
Introduzione all'algoritmo DFS
DFS è noto come algoritmo di ricerca della prima profondità che fornisce i passaggi per attraversare ogni singolo nodo di un grafico senza ripetere alcun nodo. Questo algoritmo è lo stesso di Depth First Traversal per un albero ma differisce nel mantenere un valore booleano per verificare se il nodo è già stato visitato o meno. Questo è importante per l'attraversamento del grafico, poiché nel grafico esistono anche dei cicli. In questo algoritmo viene mantenuto uno stack per memorizzare i nodi sospesi durante l'attraversamento. È chiamato così perché prima viaggiamo fino alla profondità di ciascun nodo adiacente e quindi continuiamo a percorrere un altro nodo adiacente.
Spiega l'algoritmo DFS
Questo algoritmo è contrario all'algoritmo BFS in cui sono visitati tutti i nodi adiacenti seguiti dai vicini ai nodi adiacenti. Inizia a esplorare il grafico da un nodo e ne esplora la profondità prima di tornare indietro. Due cose sono considerate in questo algoritmo:
- Visitare un vertice: selezione di un vertice o nodo del grafico da attraversare.
- Esplorazione di un vertice: attraversare tutti i nodi adiacenti a quel vertice.
Pseudo codice per la prima ricerca della profondità :
proc DFS_implement(G, v):
let St be a stack
St.push(v)
while St has elements
v = St.pop()
if v is not labeled as visited:
label v as visited
for all edge v to w in G.adjacentEdges(v) do
St.push(w)
Traversal lineare esiste anche per DFS che può essere implementato in 3 modi:
- Preordinare
- In ordine
- postorder
Il postordine inverso è un modo molto utile per attraversare e utilizzare l'ordinamento topologico e varie analisi. Viene inoltre gestito uno stack per memorizzare i nodi la cui esplorazione è ancora in sospeso.
Traversa del grafico in DFS
In DFS, i passaggi seguenti sono seguiti per attraversare il grafico. Ad esempio, un dato grafico, iniziamo l'attraversamento da 1:
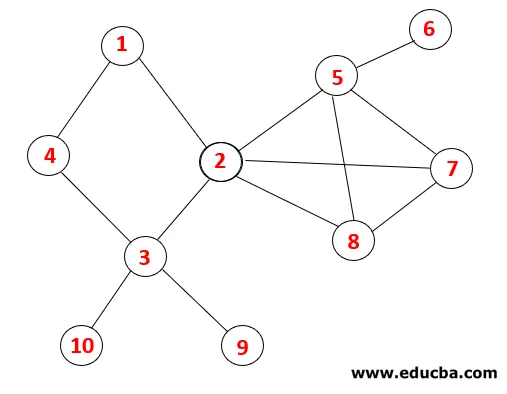
| Pila | Sequenza trasversale | Spanning Tree |
| 1 |  |
|
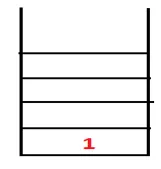 | 1, 4 |  |
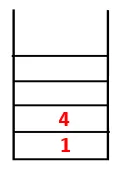 | 1, 4, 3 |  |
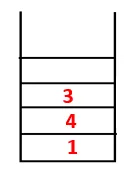 | 1, 4, 3, 10 | 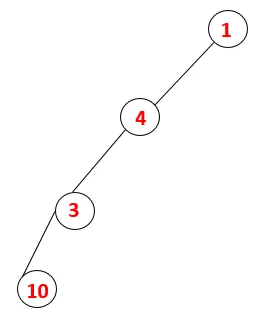 |
 | 1, 4, 3, 10, 9 | 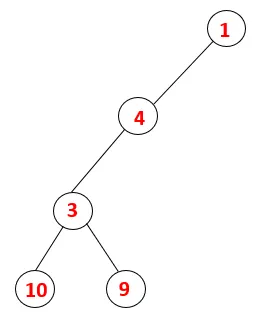 |
 | 1, 4, 3, 10, 9, 2 | 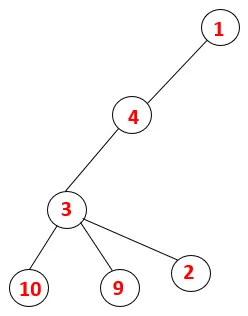 |
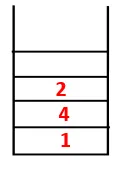 | 1, 4, 3, 10, 9, 2, 8 |  |
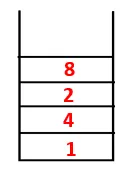 | 1, 4, 3, 10, 9, 2, 8, 7 | 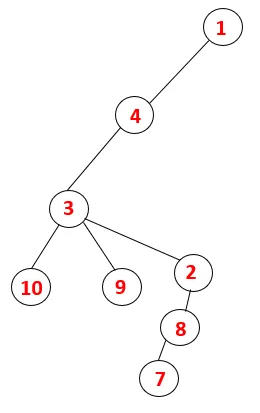 |
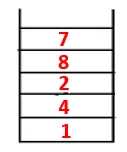 | 1, 4, 3, 10, 9, 2, 8, 7, 5 |  |
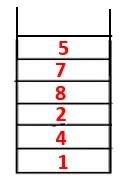 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 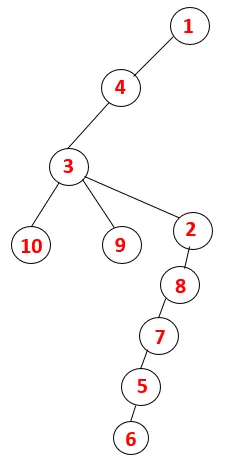 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 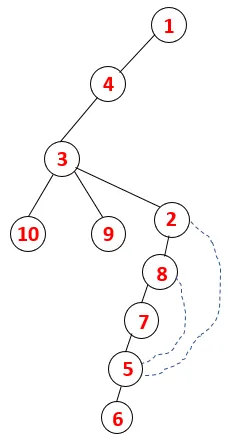 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
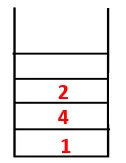 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 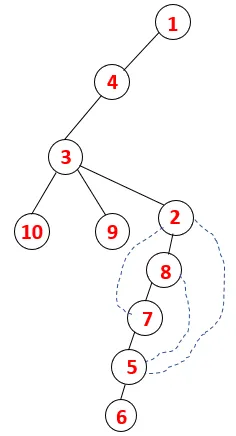 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 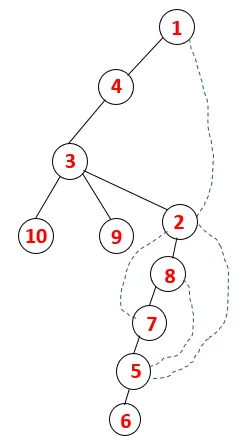 |
Spiegazione dell'algoritmo DFS
Di seguito sono riportati i passaggi per l'algoritmo DFS con vantaggi e svantaggi:
Step1: Il nodo 1 viene visitato e aggiunto alla sequenza e all'albero di spanning.
Step2: Vengono esplorati i nodi adiacenti di 1 che è 4, quindi 1 viene spinto per impilare e 4 viene spinto nella sequenza, oltre a spanning tree.
Step3: viene esplorato uno dei nodi adiacenti di 4 e quindi 4 viene spinto nella pila e 3 entra nella sequenza e si estende sull'albero.
Step4: I nodi adiacenti di 3 vengono esplorati spingendolo sullo stack e 10 entra nella sequenza. Poiché non esiste un nodo adiacente a 10, quindi 3 viene estratto dallo stack.
Passaggio 5: viene esplorato un altro nodo adiacente di 3 e 3 viene inserito nello stack e viene visitato 9. Nessun nodo adiacente di 9 quindi 3 viene espulso e viene visitato l'ultimo nodo adiacente di 3 cioè 2.
Un processo simile è seguito per tutti i nodi fino a quando lo stack diventa vuoto, il che indica la condizione di arresto per l'algoritmo di attraversamento. - -> le linee tratteggiate nella struttura ad albero si riferiscono ai bordi posteriori presenti nel grafico.
In questo modo, tutti i nodi nel grafico vengono attraversati senza ripetere nessuno dei nodi.
Vantaggi e svantaggi
- Vantaggi: i requisiti di memoria per questo algoritmo sono molto inferiori. Minore complessità in termini di spazio e tempo rispetto a BFS.
- Svantaggi: la soluzione non è garantita Applicazioni. Ordinamento topologico. Trovare ponti di grafico.
Esempio per implementare l'algoritmo DFS
Di seguito è riportato l'esempio per implementare l'algoritmo DFS:
Codice:
import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)
Produzione:
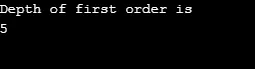
Spiegazione del programma precedente: Abbiamo creato un grafico con 5 vertici (0, 1, 2, 3, 4) e abbiamo usato l'array visitato per tenere traccia di tutti i vertici visitati. Quindi per ogni nodo i cui nodi adiacenti esistono lo stesso algoritmo si ripete fino a quando tutti i nodi sono visitati. Quindi l'algoritmo torna a chiamare il vertice e pop dallo stack.
Conclusione
Il requisito di memoria di questo grafico è inferiore rispetto a BFS in quanto è necessario mantenere solo uno stack. Di conseguenza viene generato un albero spanning DFS e una sequenza di attraversamento ma non è costante. La sequenza di attraversamento multiplo è possibile a seconda del vertice iniziale e del vertice di esplorazione scelti.
Articoli consigliati
Questa è una guida all'algoritmo DFS. Qui discutiamo passo passo della spiegazione, attraversiamo il grafico in un formato tabella con vantaggi e svantaggi. Puoi anche consultare i nostri altri articoli correlati per saperne di più -
- Che cos'è HDFS?
- Algoritmi di apprendimento profondo
- Comandi HDFS
- Algoritmo SHA