
Differenza tra il punteggio Z e il punteggio T.
Il punteggio Z è una conversione di dati grezzi in un punteggio standard, quando la conversione si basa sulla media della popolazione e sulla deviazione standard della popolazione. Quando un set di dati completo è disponibile con noi, possiamo calcolare il punteggio Z. Il punteggio Z è la sottrazione della media della popolazione dal punteggio grezzo e quindi divide il risultato con la deviazione standard della popolazione. Il punteggio T è una conversione dei dati grezzi nel punteggio standard quando la conversione si basa sulla media del campione e sulla deviazione standard del campione. Quando il set di dati sulla popolazione non è disponibile, dobbiamo raccogliere alcuni dati di esempio per calcolare la media del campione e la deviazione standard della popolazione.
Punteggio Z.
In una distribuzione normale, dove sono disponibili dati completi, è una distanza dalla media. La sua formula è indicata di seguito,
Z= (x-μ)/σ
Dove,
X = dati grezzi individuali
μ = Media della popolazione
σ = Deviazione standard della popolazione
Punteggio T.
Il punteggio T è la sottrazione della deviazione standard individuale dalla media individuale e quindi dividere il risultato con la deviazione standard del campione intero risultato moltiplicato per la dimensione del campione. La sua formula è indicata di seguito,
t = ((- μ)/s)*
= media campionaria
μ = media della popolazione
s = Deviazione standard del campione
n = dimensione del campione
Facciamo un esempio per capire meglio lo stesso:
In un documento, ci sono 3 suddivisioni: I, II e III. Consenti al numero di studenti che hanno risposto che sarò correttamente del 25%, cioè il 75% non è in grado di rispondere correttamente. Allo stesso modo, il 10% e il 20% del numero di persone che hanno risposto correttamente alle sezioni II e III, quindi il 90% e l'80% hanno trovato le sezioni II e III. Partiamo dal presupposto che l'abilità misurata da questi tre oggetti è la stessa ed è normalmente distribuita,
Il punteggio per ogni studente in una classe viene utilizzato per calcolare la media dei voti che è uguale a 50 e una deviazione standard di 10. Possiamo calcolare il punteggio Z con il punteggio di 50 come (50-50) / 10 = 0
Possiamo interpretare che il punteggio dello studente è 0 distanza (in unità di deviazioni standard) dalla media, quindi lo studente ha ottenuto un punteggio medio.
Se il punteggio è 60, il punteggio Z è (60-50) / 10 = 1
Possiamo interpretare che lo studente ha ottenuto un punteggio superiore alla media - una distanza di 1 deviazione standard sopra la media.
Confronto testa a testa tra il punteggio Z e il punteggio T (infografica)
Di seguito è riportata la principale differenza 9 tra il punteggio Z e il punteggio T. 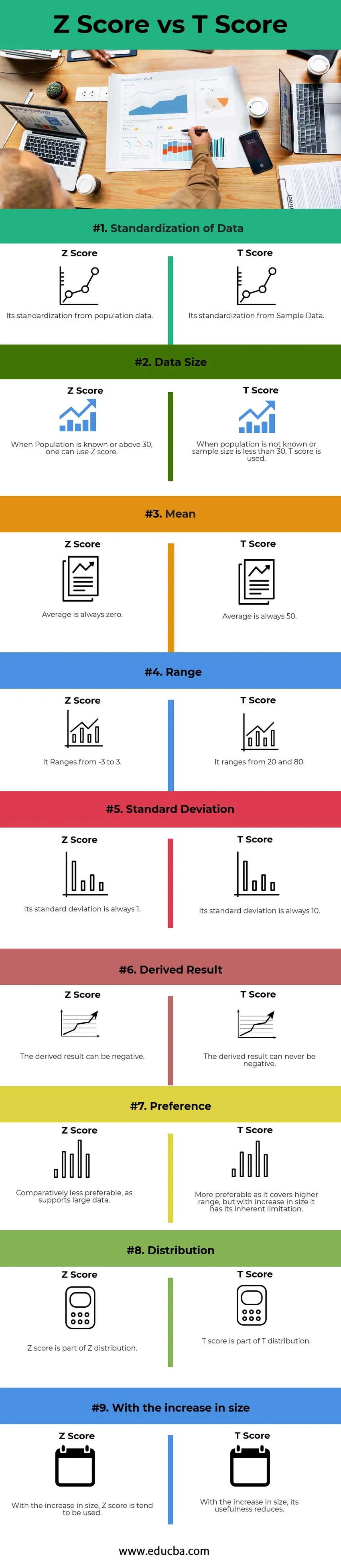
Differenze chiave tra il punteggio Z e il punteggio T.
Discutiamo alcune delle principali differenze tra il punteggio Z e il punteggio T.
- Il punteggio Z è la standardizzazione dai dati grezzi della popolazione o più di 30 dati campione al punteggio standard mentre il punteggio T è la standardizzazione dai dati campione di meno di 30 dati al punteggio standard
- Il punteggio Z varia da -3 a 3, mentre il punteggio T varia da 20 a 80.
- All'aumentare della dimensione dei dati, la distribuzione tende ad essere la distribuzione Z. Sia il punteggio Z che la distribuzione del punteggio T fanno parte di una distribuzione normale, ma in base alla dimensione differiscono l'una dall'altra
- In pratica, il punteggio Z viene ampiamente utilizzato nei dati di borsa e per verificare le possibilità di fallimento di una società, mentre il punteggio t viene ampiamente utilizzato nel controllo della densità minerale ossea e nelle valutazioni del rischio di frattura
Punteggio Z contro T Punteggio Tabella comparativa
Diamo un'occhiata ai primi 9 Confronti tra il punteggio Z e il punteggio T.
| Sr. No. | Punti di confronto | Punteggio Z | Punteggio T. |
| 1 | Standardizzazione dei dati | La sua standardizzazione dai dati sulla popolazione | La sua standardizzazione dai dati di esempio |
| 2 | Dimensione dei dati | Quando la popolazione è nota o superiore a 30, si può usare il punteggio Z. | Quando la popolazione non è nota o la dimensione del campione è inferiore a 30, viene utilizzato il punteggio T. |
| 3 | Significare | Una media è sempre zero. | Una media è sempre 50. |
| 4 | Gamma | Va da -3 a 3. | Si va da 20 a 80. |
| 5 | Deviazione standard | La sua deviazione standard è sempre 1 | La sua deviazione standard è sempre 10 |
| 6 | Risultato derivato | Il risultato derivato può essere negativo | Il risultato derivato non può mai essere negativo |
| 7 | Preferenza | Comparativamente meno preferibile, poiché supporta dati di grandi dimensioni | Più preferibile in quanto copre una gamma più alta, ma con un aumento delle dimensioni ha il suo limite intrinseco |
| 8 | Distribuzione | Il punteggio Z fa parte della distribuzione Z. | Il punteggio T fa parte della distribuzione T. |
| 9 | Con l'aumento delle dimensioni | Con l'aumento delle dimensioni, il punteggio Z tende ad essere utilizzato | Con l'aumento delle dimensioni, la sua utilità si riduce. |
Conclusione
Sia il punteggio Z che il punteggio T fanno parte del test di ipotesi nella distribuzione normale. Se si dispone di una serie di punteggi di misurazione su diverse misure utilizzando i punteggi Z, è possibile sapere come vengono posizionati i punteggi nelle loro distribuzioni. Quindi puoi confrontarli. La standardizzazione dei punteggi è una procedura ampiamente utilizzata nel campo della ricerca e della pianificazione in quanto aiutano a confrontare i vari punteggi dei test. La standardizzazione dei punteggi prima di combinarli aiuta un ricercatore a ottenere risultati migliori e comparabili.
Articoli consigliati
Questa è stata una guida alla differenza principale tra il punteggio Z e il punteggio T. Qui discutiamo anche le differenze chiave tra il punteggio Z e il punteggio T con infografica e tabella di confronto. Puoi anche dare un'occhiata ai seguenti articoli per saperne di più-
- Finanza vs economia - Massima differenza
- Deficit vs Debt - Qual è il migliore
- Acquisto di beni contro acquisto di titoli
- Mercato monetario vs mercato dei capitali
- Panoramica del punteggio Altman Z.