
Formula del punteggio Z (sommario)
- Formula
- Esempi
- Calcolatrice
Cos'è la formula del punteggio Z?
Il "punteggio Z" è uno degli strumenti statistici più utilizzati che viene utilizzato per standardizzare il punteggio, purché siano noti i mezzi della popolazione e la deviazione standard. Pertanto, il punteggio Z è anche noto come punteggio standard. Il punteggio Z varia nell'intervallo di -3 volte la deviazione standard a +3 volte la deviazione standard con una media di zero e una deviazione standard di uno. La formula per il punteggio Z di una variabile può essere derivata deducendo la media della popolazione dalla variabile data (che fa parte del set di dati o della popolazione) e quindi dividendo il risultato per la deviazione standard della popolazione. Matematicamente, è rappresentato come,
Z = (X – μ) / σ
dove,
- X = Variabile dalla popolazione
- μ = media della popolazione
- σ = Deviazione standard della popolazione
Esempi di formula del punteggio Z (con modello Excel)
Facciamo un esempio per comprendere meglio il calcolo del punteggio Z.
Puoi scaricare questo modello Excel Formula punteggio Z qui - Modello Excel formula punteggio ZFormula del punteggio Z - Esempio n. 1
Prendiamo l'esempio di Manny che recentemente è apparso per SAT. È riuscito a segnare 1109 in questo tentativo. Tuttavia, secondo le informazioni disponibili, il punteggio medio per SAT è rimasto intorno al 1030 con una deviazione standard di 250. Calcola il punteggio Z per il punteggio SAT di Manny e valuta quanto ha fatto rispetto ai media dei partecipanti al test.
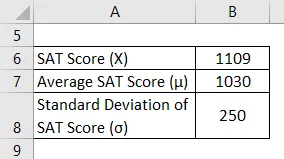
Soluzione:
Il punteggio Z viene calcolato utilizzando la formula indicata di seguito
Z = (X - μ) / σ
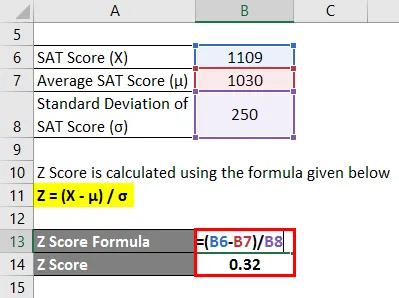
- Punteggio Z = (1109 - 1030) / 250
- Punteggio Z = 0, 32
Pertanto, il punteggio SAT di Manny è 0, 32 deviazione standard superiore al punteggio medio dei partecipanti al test, il che indica che il 62, 55% dei partecipanti al test ha ottenuto un punteggio inferiore a Manny.
Formula del punteggio Z - Esempio n. 2
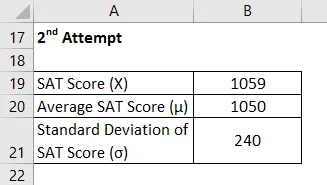
Ora, prendiamo l'esempio del Chelsea che ha scritto due volte la SAT e vuole confrontare la sua prestazione in esse. È riuscita a segnare 1085 e 1059 rispettivamente nei suoi 1 ° e 2 ° tentativo. Secondo le informazioni disponibili, il punteggio medio e la deviazione standard durante il 1 ° tentativo erano rispettivamente di 1100 e 230, mentre in quest'ultimo erano rispettivamente di 1050 e 240. Aiuta Chelsea a decidere in quale esame ha ottenuto risultati migliori.
Soluzione:
1 ° tentativo
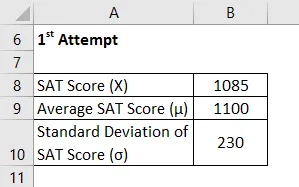
Il punteggio Z viene calcolato utilizzando la formula indicata di seguito
Z = (X - μ) / σ
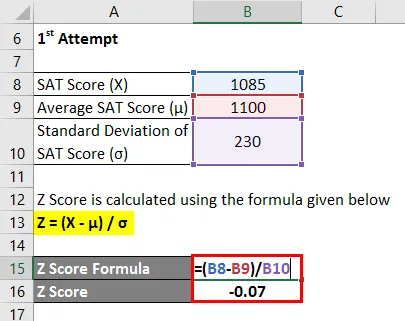
- Punteggio Z = (1085-1100) / 230
- Punteggio Z = -0, 07
Pertanto, il punteggio SAT del Chelsea nel 1 ° tentativo è 0, 07 deviazione standard inferiore al punteggio medio dei partecipanti al test, il che indica che il 47, 40% dei partecipanti al test ha segnato meno del Chelsea durante il 1 ° tentativo.
2 ° tentativo
Il punteggio Z viene calcolato utilizzando la formula indicata di seguito
Z = (X - μ) / σ
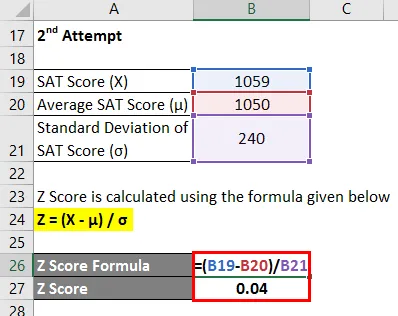
- Punteggio Z = (1059 - 1050) / 240
- Punteggio Z = 0, 04
Pertanto, il punteggio SAT del Chelsea nel secondo tentativo è 0, 04 deviazione standard superiore al punteggio medio dei partecipanti al test, il che indica che il 51, 50% dei partecipanti al test ha segnato meno del Chelsea durante il secondo tentativo.
Quindi, dal confronto dei punteggi Z, è chiaro che il Chelsea ha ottenuto risultati migliori durante il suo secondo tentativo.
Spiegazione
La formula per il punteggio Z può essere derivata utilizzando i seguenti passaggi:
Passaggio 1: in primo luogo, costruire una popolazione con un gran numero di variabili e le variabili sono indicate da X i .
Passaggio 2: Successivamente, viene calcolato il numero di variabili nella popolazione ed è indicato da N.
Passaggio 3: Successivamente, la media della popolazione viene calcolata sommando tutte le variabili seguite dalla divisione per il numero totale di variabili (passaggio 2) nel set di dati. La media della popolazione è indicata con μ.
μ = ∑ X i / N
Passaggio 4: Successivamente, dedurre la media da ciascuna variabile del set di dati per calcolare la loro deviazione dalla media.
cioè (X i - μ) è la deviazione per l'i esimo punto dati.
Passaggio 5: Successivamente, calcolare le deviazioni al quadrato per le variabili, ovvero (X i - μ) 2 .
Passaggio 6: Successivamente, sommare tutte le deviazioni al quadrato e quindi dividere il totale per il numero di variabili nel set di dati per arrivare alla varianza.
σ 2 = ∑ (X i - μ) 2 / N
Passaggio 7: Successivamente, la deviazione standard della popolazione viene calcolata calcolando la radice quadrata della varianza calcolata nel passaggio precedente.
σ = √ ∑ (X i - μ) 2 / N
Passaggio 8: Infine, la formula per il punteggio Z viene derivata deducendo la media della popolazione (passaggio 3) dalla variabile e quindi dividendo il risultato per la deviazione standard della popolazione (passaggio 7) come mostrato di seguito.
Z = (X - μ) / σ
Pertinenza e usi della formula del punteggio Z.
Dal punto di vista di uno statistico, il concetto di punteggio Z è molto importante in quanto è utile per determinare la probabilità che si verifichi o meno un evento all'interno di una distribuzione normale. In effetti, il punteggio Z viene utilizzato anche per confrontare due punteggi grezzi di due diverse distribuzioni normali ed è fatto convertendo i punteggi grezzi in punteggio Z o punteggio standardizzato. Inoltre, un punteggio Z positivo implica un punteggio superiore alla media, mentre un punteggio Z negativo implica un punteggio inferiore alla media.
Z Score Calculator Calculator
È possibile utilizzare il seguente calcolatore della formula del punteggio Z
| X | |
| μ | |
| σ | |
| Z | |
| Z = |
|
|
Articoli consigliati
Questa è stata una guida alla formula del punteggio Z. Qui discutiamo come calcolare il punteggio Z insieme ad esempi pratici. Forniamo anche un calcolatore del punteggio Z con modello Excel scaricabile. Puoi anche consultare i seguenti articoli per saperne di più -
- Esempi di formula delle dimensioni del campione
- Come calcolare la media ponderata?
- Calcolatrice per la formula di correlazione
- Formula per calcolare la distribuzione normale
- Esempi di Altman Z Score