
Coefficiente di formula di variazione (sommario)
- Formula
- Esempi
Qual è il coefficiente della formula di variazione?
In statistica, il coefficiente di variazione chiamato anche CV è uno strumento che ci aiuta a determinare come i punti di dati in un set di dati sono distribuiti attorno alla media. Fondamentalmente, tutti i punti dati vengono prima tracciati e quindi il coefficiente di variazione viene utilizzato per misurare la dispersione di tali punti l'uno dall'altro e la media. Quindi ci aiuta a comprendere i dati e anche a vedere il modello che formano. Viene calcolato come rapporto tra la deviazione standard del set di dati e il valore medio. Un coefficiente di variazione più elevato significa che esiste un livello maggiore di dispersione dei dati attorno alla media. Allo stesso modo, più basso è il valore del coefficiente di variazione, minore è la dispersione e più precisi saranno i risultati. Anche se la media di due serie di dati è considerevolmente diversa, il coefficiente di variazione è molto utile per confrontare il grado di variazione da una serie di dati all'altra.
La formula per il coefficiente di variazione è data da:
Coefficient of Variation = Standard Deviation / Mean
Passaggi per calcolare il coefficiente di variazione:
Passaggio 1: calcolare la media del set di dati. La media è la media di tutti i valori e può essere calcolata prendendo la somma di tutti i valori e quindi dividendola per un numero di punti dati.
Passaggio 2: quindi calcolare la deviazione standard del set di dati. Questo è un processo che richiede poco tempo. La deviazione standard può essere calcolata come: √ (Σ (X i - X m ) 2 / (n - 1)) . X i è il punto di dati ith e X m è la media del set di dati. In alternativa, possiamo anche trovare la deviazione standard in Excel utilizzando la funzione STDEV.S ().
Passaggio 3: dividere la deviazione standard per media per ottenere il coefficiente di variazione.
Esempi di coefficiente di formula di variazione (con modello di Excel)
Facciamo un esempio per comprendere meglio il calcolo del coefficiente di variazione.
Puoi scaricare questo modello Excel di coefficiente di variazione della formula qui - Modello Excel di coefficiente di variazione della formulaCoefficiente di formula di variazione - Esempio n. 1
Diciamo che abbiamo due set di dati A e B e ognuno contiene 20 punti dati casuali. Calcola il coefficiente di variazione per il set di dati X e Y.
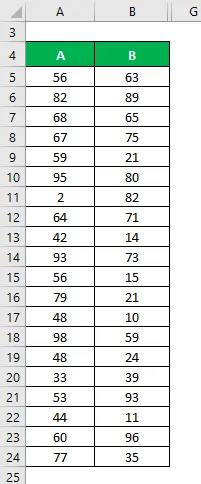
Soluzione:
La media è calcolata come:
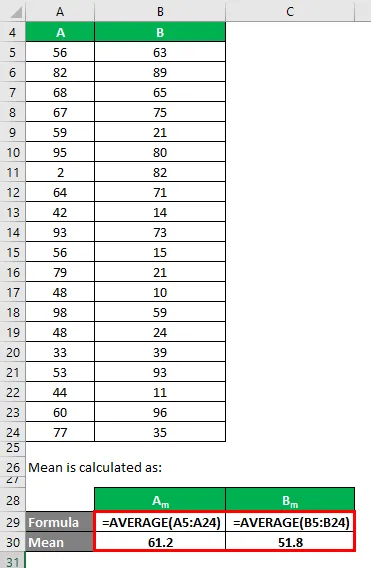
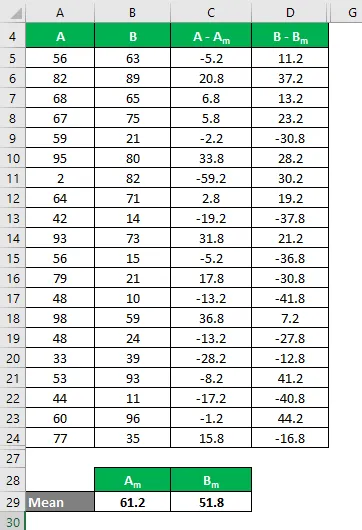
- Media del set di dati A = 61.2
- Media del set di dati B = 51, 8
Ora, dobbiamo calcolare la differenza tra i punti dati e il valore medio.
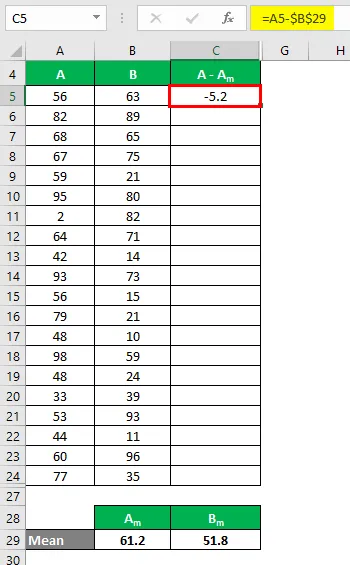
Allo stesso modo, calcolare per tutti i valori del set di dati A.
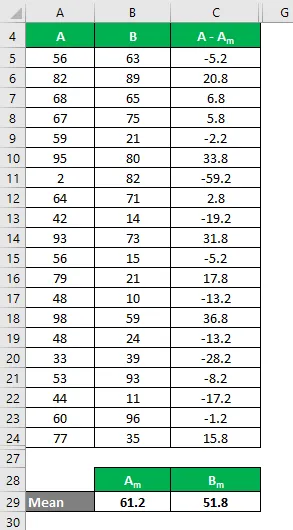
Allo stesso modo, calcolare per tutti i valori del set di dati B.
Calcola il quadrato della differenza per entrambi i set di dati A e B.
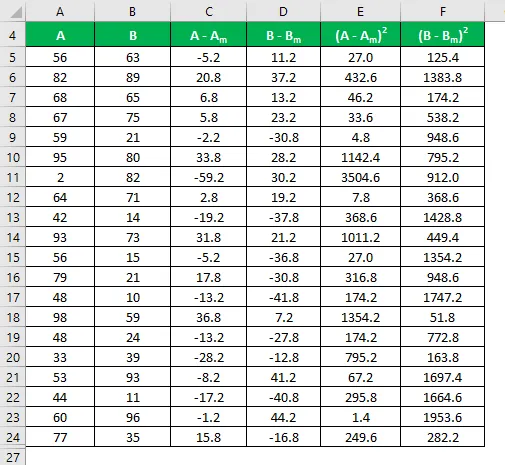
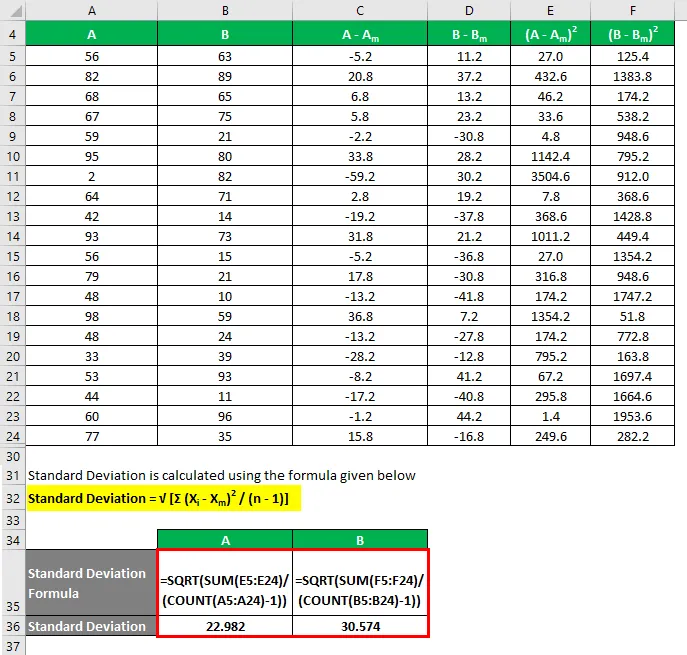
La deviazione standard viene calcolata utilizzando la formula indicata di seguito
Deviazione standard = √ (Σ (X i - X m ) 2 / (n - 1))
Il coefficiente di variazione viene calcolato utilizzando la formula indicata di seguito
Coefficiente di variazione = Deviazione standard / media
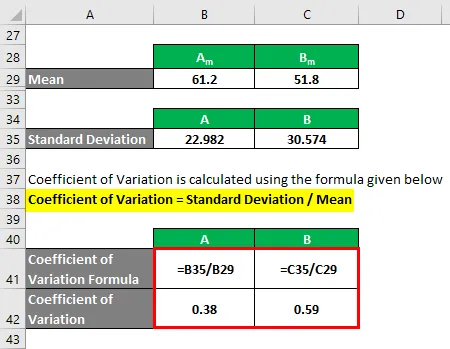
- Coefficiente di variazione A = 22.982 / 61.2 = 0.38
- Coefficiente di variazione B = 30.574 / 51, 8 = 0, 59
Quindi, se vedi qui, B ha un coefficiente di variazione maggiore di A, il che significa che i punti dati di B sono più dispersi di A.
Coefficiente di formula di variazione - Esempio n. 2
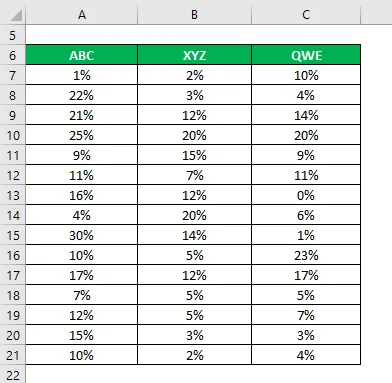
Diciamo che sei un investitore molto avverso al rischio e stai cercando di investire denaro nel mercato azionario. Poiché la tua propensione al rischio è bassa, vuoi investire in titoli sicuri che hanno una deviazione standard e un coefficiente di variazione inferiori. Hai selezionato 3 azioni in base alle loro informazioni tecniche e fondamentali e vuoi scegliere 2 azioni. Hai anche raccolto informazioni sui loro rendimenti storici negli ultimi 15 anni.
Soluzione:
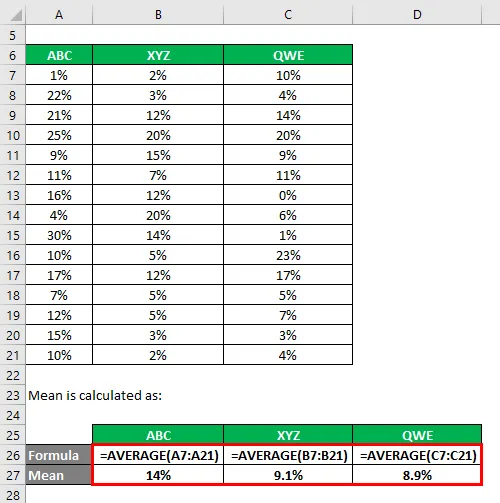
La media è calcolata come:
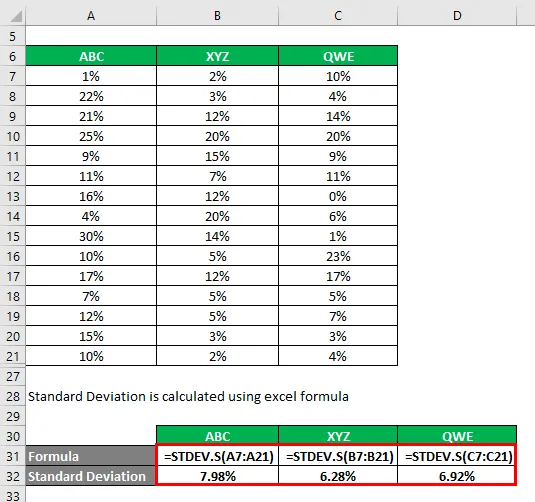
La deviazione standard viene calcolata utilizzando la formula di Excel
Il coefficiente di variazione viene calcolato utilizzando la formula indicata di seguito
Coefficiente di variazione = Deviazione standard / media
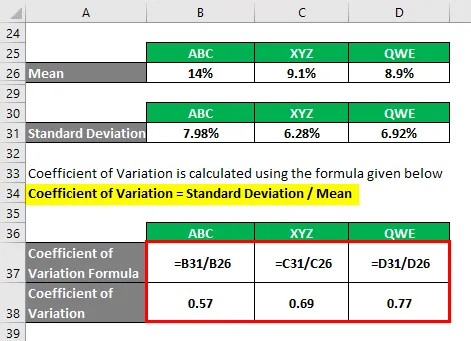
- Coefficiente di variazione ABC = 7, 98% / 14% = 0, 57
- Coefficiente di variazione XYZ = 6, 28% / 9, 1% = 0, 69
- Coefficiente di variazione QWE = 6, 92% / 8, 9% = 0, 77
Sulla base delle informazioni, sceglierai le azioni ABC e XYZ da investire poiché hanno il coefficiente di variazione più basso.
Spiegazione
Poiché il coefficiente di variazione è una misura del rischio, aiuta a misurare la volatilità dei prezzi delle azioni e di altri strumenti finanziari. Aiuta inoltre investitori e analisti a confrontare i rischi associati a diversi potenziali investimenti.
Il coefficiente di variazione è simile alla deviazione standard ma una deviazione standard di due variabili non può essere confrontata in utile. L'uso della deviazione standard e della media rende il confronto relativo più significativo. Esiste anche una limitazione del coefficiente di variazione. Supponiamo che la media di un set di dati sia zero. In tal caso, questo strumento diventerà inefficace. Non solo, se disponiamo di un set di dati con molti valori positivi e negativi, il coefficiente di variazione diventa molto problematico. Quindi è solo più utile con set di dati con lo stesso segno più-meno.
Rilevanza e usi del coefficiente di formula di variazione
Il coefficiente di variazione ha rilevanza in molti altri campi diversi dalle statistiche. Ad esempio, nel campo della finanza, il coefficiente di variazione è una misura del rischio. È simile alla deviazione standard poiché viene utilizzato anche come misura del rischio, ma la differenza è che il coefficiente di variazione è un indicatore migliore del rischio relativo. Ad esempio, supponiamo che il rendimento atteso di A del 15% e il rendimento atteso di B del 10% e A abbia una deviazione standard del 10%, mentre B abbia una deviazione standard del 5%. Per scegliere un investimento migliore, è possibile utilizzare il coefficiente di variazione. Quindi il coefficiente di variazione di A è 10/15 = 0, 666 e il coefficiente di variazione di B è 5/10 = 0, 5. Quindi B è un investimento migliore di A.
Articoli consigliati
Questa è stata una guida al coefficiente di formula di variazione. Qui discutiamo come calcolare il coefficiente di variazione usando la formula insieme ad esempi pratici e template Excel scaricabili. Puoi anche consultare i seguenti articoli per saperne di più -
- Che cos'è la formula quadrata R rettificata?
- Esempi di formula del coefficiente di determinazione
- Come calcolare il coefficiente di correlazione usando la formula?
- Formula di covarianza con modello di Excel