
Introduzione alle funzioni in R
La funzione è definita come un insieme di istruzioni, per eseguire e svolgere qualsiasi attività logica specifica. La funzione accetta alcuni parametri di input che sono noti come argomenti per eseguire tale attività. Le funzioni aiutano a spezzare il codice, in blocchi più semplici orchestrandolo logicamente, che è più facile da leggere e comprendere. In questo argomento, impareremo le funzioni in R.
Come scrivere funzioni in R?
Per scrivere la funzione in R, ecco la sintassi:
Fun_name <- function (argument) (
Function body
)
Qui, si può vedere la parola riservata specifica “funzione” in R, per definire qualsiasi funzione. La funzione accetta input che si presenta sotto forma di argomenti. Il corpo della funzione è un insieme di istruzioni logiche eseguite su argomenti e quindi restituisce l'output. "Fun_name" è il nome assegnato alla funzione, attraverso la quale può essere chiamato in qualsiasi punto del programma R.
Vediamo un esempio, che sarà più lucido nel comprendere il concetto di funzione in R.
Codice R.
Multi <- function(x, y) (
# function to print x multiply y
result <- x*y
print(paste(x, "Multiply", y, "is", result))
)
produzione:
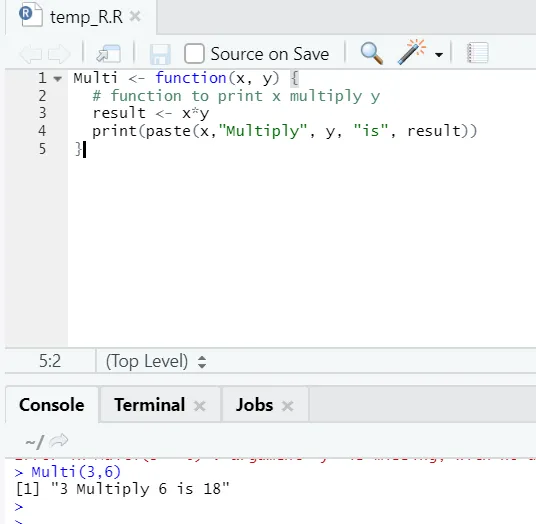
Qui abbiamo creato il nome della funzione "Multi", che accetta due argomenti come input e fornisce l'output moltiplicato. Il primo argomento è x e il secondo argomento è y. Come puoi vedere, abbiamo chiamato la funzione con il nome "Multi". Qui se qualcuno lo desidera, gli argomenti possono anche essere impostati sul valore predefinito.
Diversi tipi di funzioni in R
Diverse funzioni R con sintassi ed esempi (built-in, matematica, statistica, ecc.)
1) Funzione integrata -
Queste sono le funzioni fornite con R per affrontare un'attività specifica prendendo un argomento come input e fornendo un output basato sull'input dato. Discutiamo alcune importanti funzioni generali di R qui:
a) Ordinamento: i dati possono essere dell'ordinamento in ordine crescente o decrescente. I dati possono essere se un vettore di variabile continua o variabile di fattore.
Sintassi:

Ecco la spiegazione dei suoi parametri:
- x: questo è un vettore della variabile continua o variabile del fattore
- decrescente: può essere impostato su Vero / Falso per controllare l'ordine in ordine crescente o decrescente. Di default, è FALSE`.
- last: se il vettore ha valori NA, deve essere inserito per ultimo o no
Codice R e output:
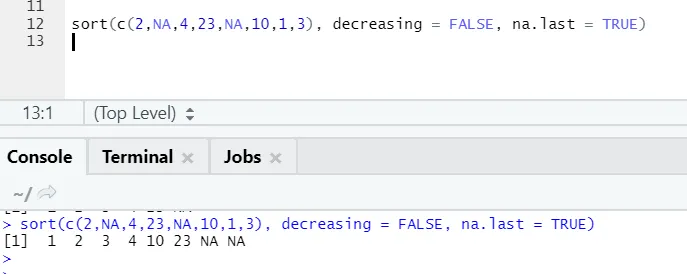
Qui si può notare come i valori "NA" vengano allineati alla fine. Poiché il nostro parametro na.last = True era vero.
b) Seq: genera una sequenza del numero tra due numeri specificati.
Sintassi
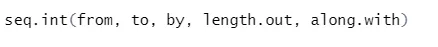
Ecco la spiegazione dei suoi parametri:
- da, per iniziare e terminare il valore della sequenza.
- di: incremento / gap tra due numeri consecutivi in sequenza
- length.out: la lunghezza richiesta della sequenza.
- Along.with: si riferisce alla lunghezza dalla lunghezza di questo argomento
Codice R e output:
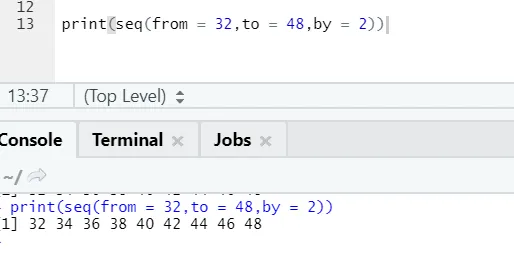
Qui si può notare che la sequenza generata ha un incremento di 2 perché by è definito come 2.
c) Toupper, tolower: le due funzioni: toupper e tolower sono funzioni applicate sulla stringa per modificare i casi delle lettere in frasi.
Codice R e output:
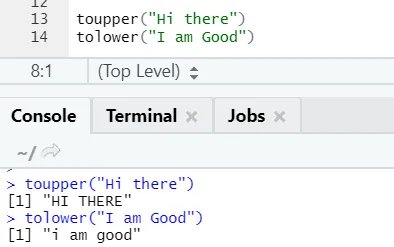
Si può notare come i casi di lettere vengano modificati quando applicati alla funzione.
d) Rnorm: questa è una funzione integrata che genera numeri casuali.
Codice R e output:
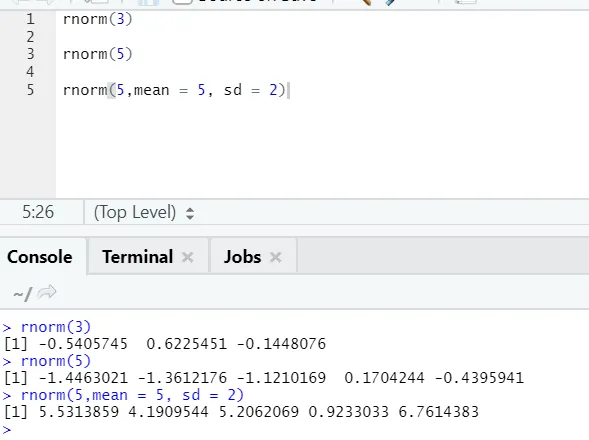
La funzione rnorm prende il primo argomento che dice quanti numeri devono essere generati.
e) Rep: questa funzione replica il valore tante volte quanto specificato.
Sintassi R: rnorm (x, n)
Qui x rappresenta il valore da replicare e n rappresenta il numero di volte che deve essere replicato.
Codice R e output:
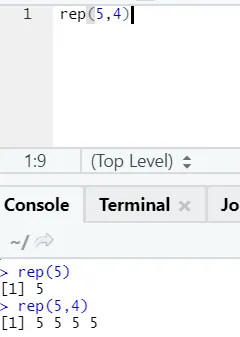
f) Incolla: questa funzione serve a concatenare le stringhe insieme a un carattere specifico nel mezzo.
sintassi
paste(x, sep = “”, collapse = NULL)
Codice R.
paste("fish", "water", sep=" - ")
Uscita R:
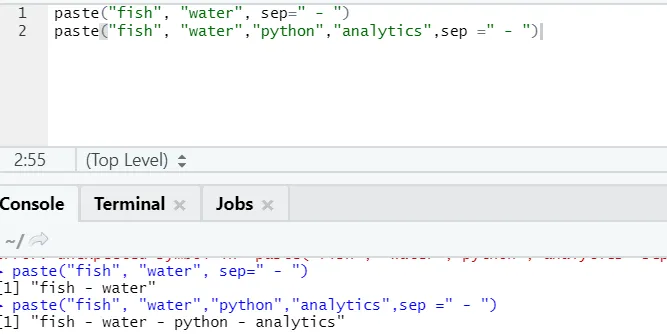
Come puoi vedere, possiamo incollare anche più di due stringhe. Sep è quel carattere specifico che abbiamo aggiunto tra le stringhe. Per impostazione predefinita, sep è spazio.
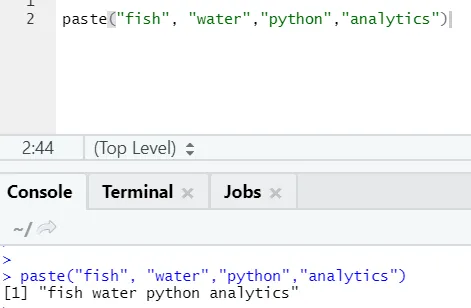
Esiste un'altra funzione simile come questa, di cui tutti dovrebbero essere a conoscenza è paste0.
La funzione paste0 (x, y, collapse) funziona in modo simile a paste (x, y, sep = “”, collapse)
Vedi l'esempio seguente:
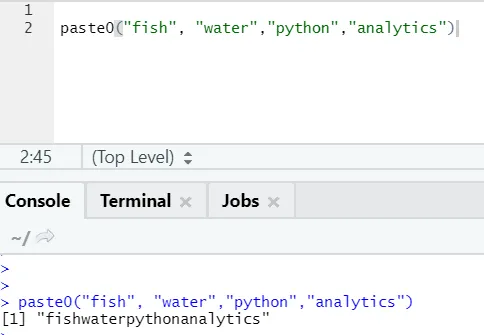
In parole semplici, per riassumere paste e paste0:
Paste0 è più veloce di paste quando si tratta della concatenazione di stringhe senza alcun separatore. Come incolla cerca sempre "sep" e che è lo spazio per impostazione predefinita in esso.
g) Strsplit: questa funzione è di dividere la stringa. Vediamo i casi semplici:
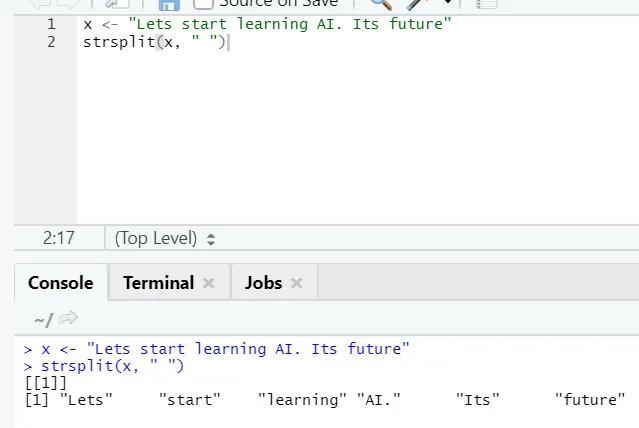
h) Rbind: la funzione rbind aiuta a pettinare i vettori con lo stesso numero di colonne, una sopra l'altra.
Esempio
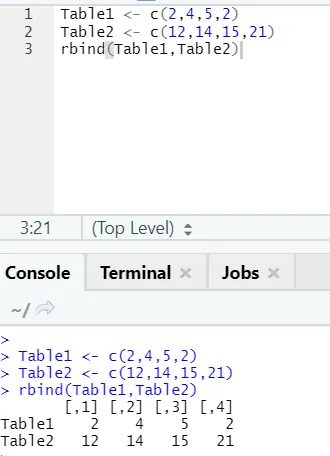
i) cbind: combina vettori con lo stesso numero di righe, fianco a fianco.
Esempio
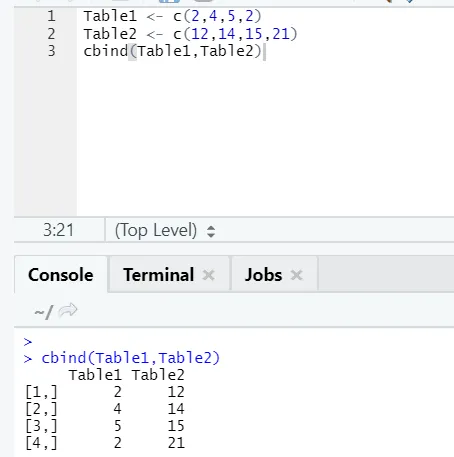
Nel caso in cui il numero di righe non corrisponda, di seguito è riportato l'errore:

Sia cbind che rbind aiutano a manipolare e rimodellare i dati.
2) Funzione matematica -
R offre una vasta gamma di funzioni matematiche. Vediamone alcuni in dettaglio:
a) Sqrt: questa funzione calcola la radice quadrata di un numero o di un vettore numerico.
Codice R e output:
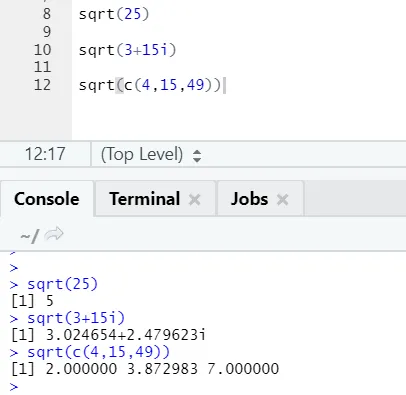
Si può vedere come è stata calcolata la radice quadrata di un numero, un numero complesso e una sequenza di vettore numerico.
b) Exp: questa funzione calcola il valore esponenziale di un numero o di un vettore numerico.
Codice R e output:
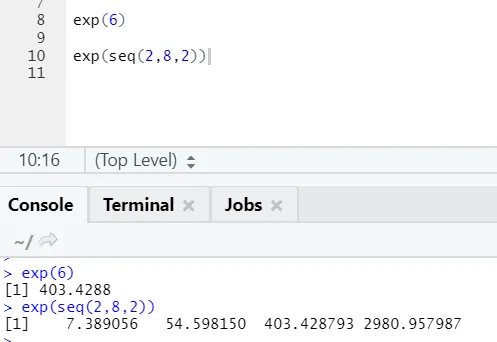
c) Cos, Sin, Tan: Queste sono funzioni di trigonometria implementate in R qui.
Codice R e output:
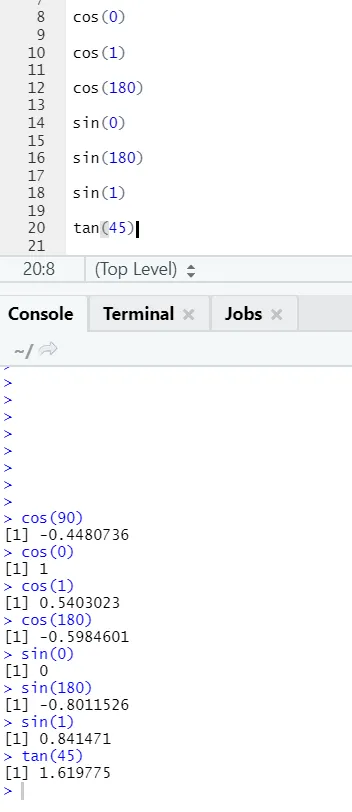
d) Abs: questa funzione restituisce il valore positivo assoluto di un numero.
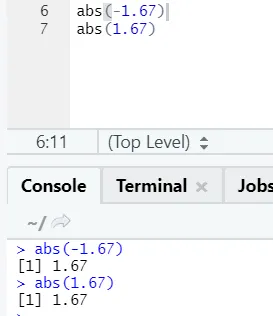
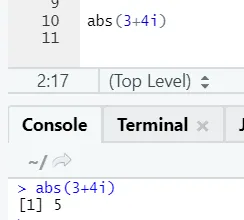
Come puoi vedere, il negativo o il positivo di un numero verranno restituiti nella sua forma assoluta. Vediamolo per un numero complesso:
e) Log: serve per trovare il logaritmo di un numero.
Ecco l'esempio che segue:
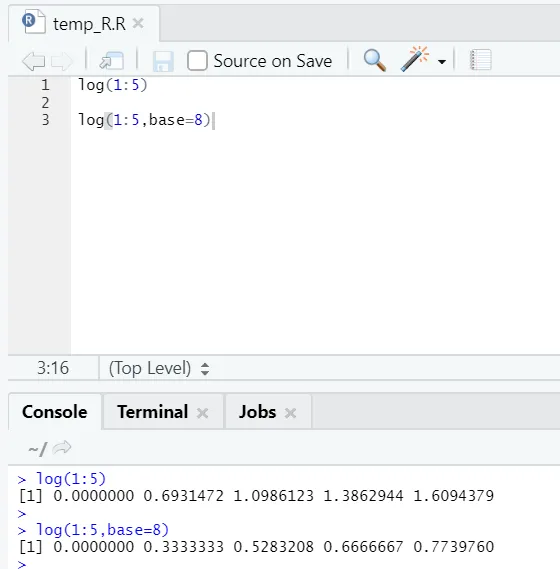
Qui si ottiene la flessibilità di cambiare la base, secondo i requisiti.
f) Cumsum: questa è una funzione matematica che fornisce somme cumulative. Ecco l'esempio seguente:
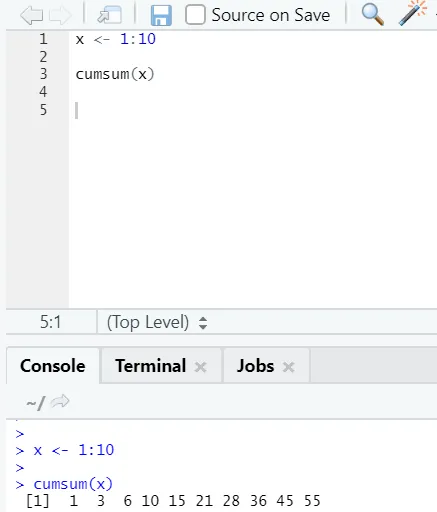
g) Cumprod: come la funzione matematica di Cumsum, abbiamo cumprod dove si verifica la moltiplicazione cumulativa.
Vedi l'esempio seguente:
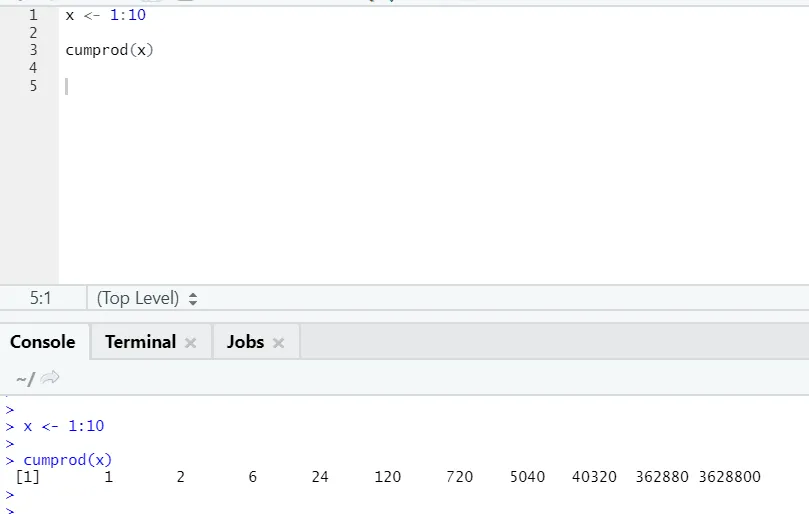
h) Max, Min: questo ti aiuterà a trovare il valore massimo / minimo nell'insieme dei numeri. Vedi sotto gli esempi relativi a questo:
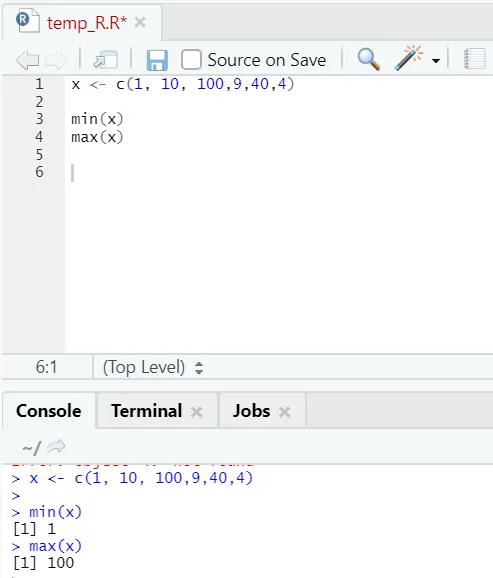
i) Soffitto: il soffitto è una funzione matematica che restituisce il più piccolo dell'intero più alto di quanto specificato.
Vediamo un esempio:
soffitto (2.67)
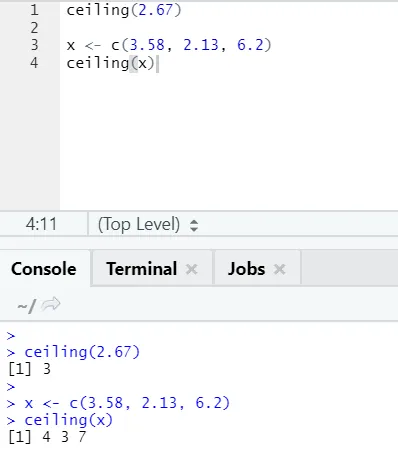
Come puoi notare, il limite viene applicato sia su un numero che su un elenco e l'output è il più piccolo dell'intero successivo più alto.
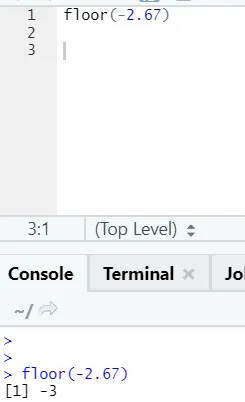
j) Piano: il piano è una funzione matematica che restituisce il valore intero più piccolo del numero specificato.
L'esempio mostrato di seguito ti aiuterà a capirlo meglio:
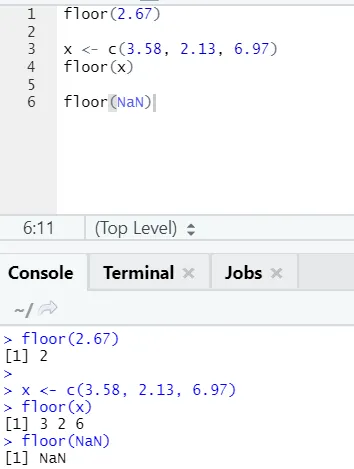
Funziona allo stesso modo anche per valori negativi. Per favore dai un'occhiata:
3) Funzioni statistiche -
Queste sono le funzioni che descrivono la relativa distribuzione di probabilità.
a) Mediana: calcolava la mediana dalla sequenza di numeri.
Sintassi
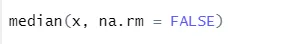
Codice R e output:
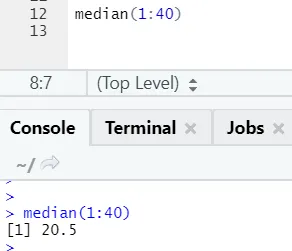
b) Dnorm: si riferisce alla distribuzione normale. La funzione dnorm restituisce il valore della funzione di densità di probabilità, per la distribuzione normale dati parametri per x, μ e σ.
Codice R e output:
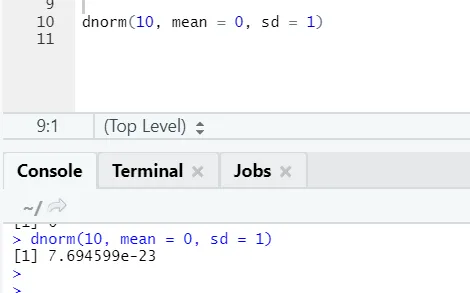
c) Cov: Covarianza dice se due vettori sono positivamente, negativamente o totalmente non correlati.
Codice R.
x_new = c(1., 5.5, 7.8, 4.2, -2.7, -5.5, 8.9)
y_new = c(0.1, 2.0, 0.8, -4.2, 2.7, -9.4, -1.9)
cov(x_new, y_new)
Uscita R:
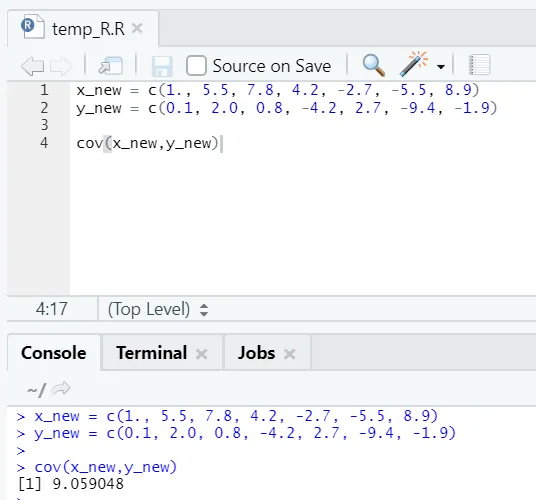
Come puoi vedere, due vettori sono correlati positivamente, il che significa che entrambi i vettori si muovono nella stessa direzione. Se la covarianza è negativa, significa che xey sono inversamente correlate e quindi si muove nella direzione opposta.
d) Cor: questa è una funzione per trovare la correlazione tra i vettori. In realtà fornisce il fattore di associazione tra i due vettori che è noto come "coefficiente di correlazione". La correlazione aggiunge un fattore di laurea rispetto alla covarianza. Se due vettori sono correlati positivamente, la correlazione ti dirà anche con quale estensione sono positivamente correlati.
Questi tre tipi di metodi che possono essere utilizzati per trovare una correlazione tra due vettori:
- Correlazione di Pearson
- Correlazione di Kendall
- Correlazione di Spearman
Nel semplice formato R, sembra che:
cor(x, y, method = c("pearson", "kendall", "spearman"))
Qui xey sono vettori.
Vediamo l'esempio pratico di correlazione su un set di dati integrato.
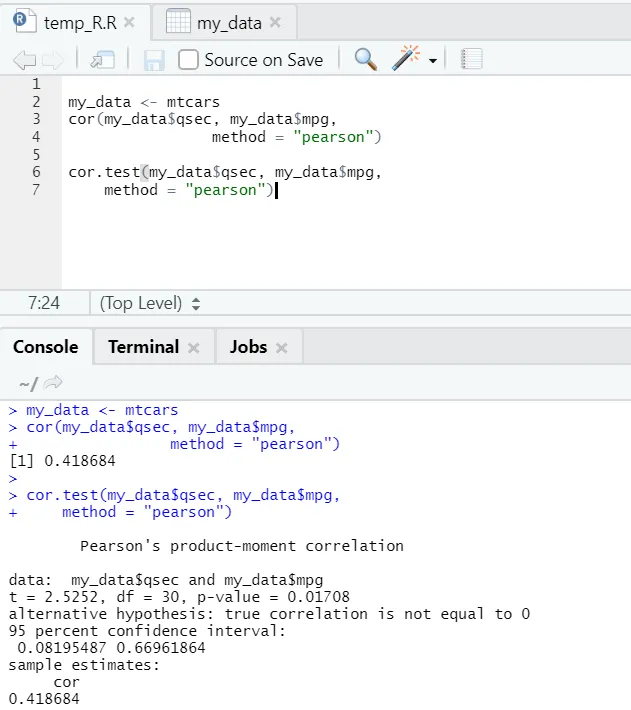
Quindi, qui puoi vedere la funzione "cor ()" che ha dato il coefficiente di correlazione 0.41 tra "qsec" e "mpg". Tuttavia, è stata anche mostrata un'altra funzione, ad esempio "cor.test ()" che non solo indica il coefficiente di correlazione ma anche il valore p e il valore t ad esso correlati. L'interpretazione diventa molto più semplice con la funzione cor.test.
Simile può essere fatto con gli altri due metodi di correlazione:
Codice R per il metodo Pearson:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = " pearson ")
cor.test(my_data$qsec, my_data$mpg, method = " pearson")
Codice R per il metodo Kendall:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = " kendall")
cor.test(my_data$qsec, my_data$mpg, method = " kendall")
Codice R per il metodo Spearman:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = "spearman")
cor.test(my_data$qsec, my_data$mpg, method = "spearman")
Il coefficiente di correlazione è compreso tra -1 e 1.
Se il coefficiente di correlazione è negativo, ciò implica che x aumenta y diminuisce.
Se il coefficiente di correlazione è zero, ciò implica che non esiste alcuna associazione tra xe y.
Se il coefficiente di correlazione è positivo, ciò implica che x aumenta anche y tende ad aumentare.
e) Test T: il test T ti dirà se due serie di dati provengono dalle stesse (supponendo) distribuzioni normali o meno.
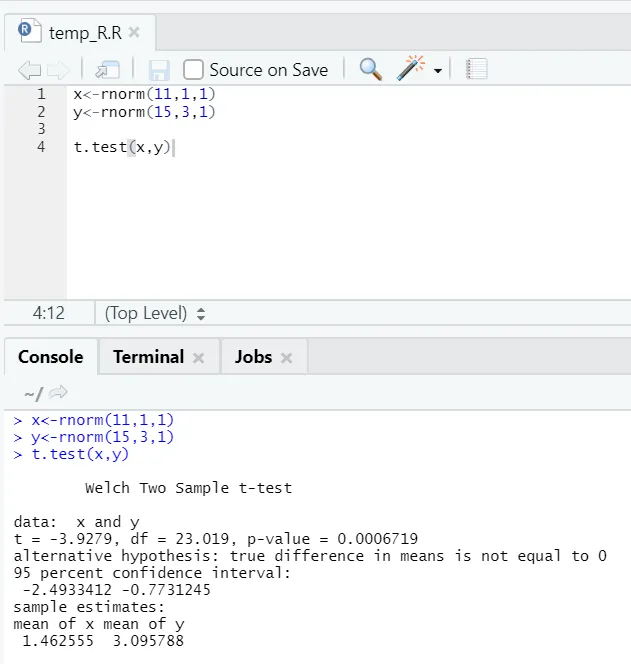
Qui dovresti respingere l'ipotesi nulla che le due medie siano uguali perché il valore p è inferiore a 0, 05.
Questa istanza mostrata è di tipo: set di dati non accoppiati con varianze disuguali. Allo stesso modo, può essere provato con il set di dati associato.
f) Regressione lineare semplice: mostra la relazione tra la variabile predittore / indipendente e risposta / dipendente.
Un semplice esempio pratico potrebbe essere la previsione del peso di una persona se si conosce l'altezza.
Sintassi R
lm(formula, data)
Qui la formula illustra la relazione tra output ie y e variabile input iex I dati rappresentano il set di dati, su cui deve essere applicata la formula.
Vediamo un esempio pratico, in cui l'area del pavimento è la variabile di input e l'affitto è la variabile di output.
x <- c (1510, 1000, 600, 500, 1280, 136, 1790, 1630)
y <- c (15000, 10000, 6000, 5000, 12800, 13600, 17900, 16300)
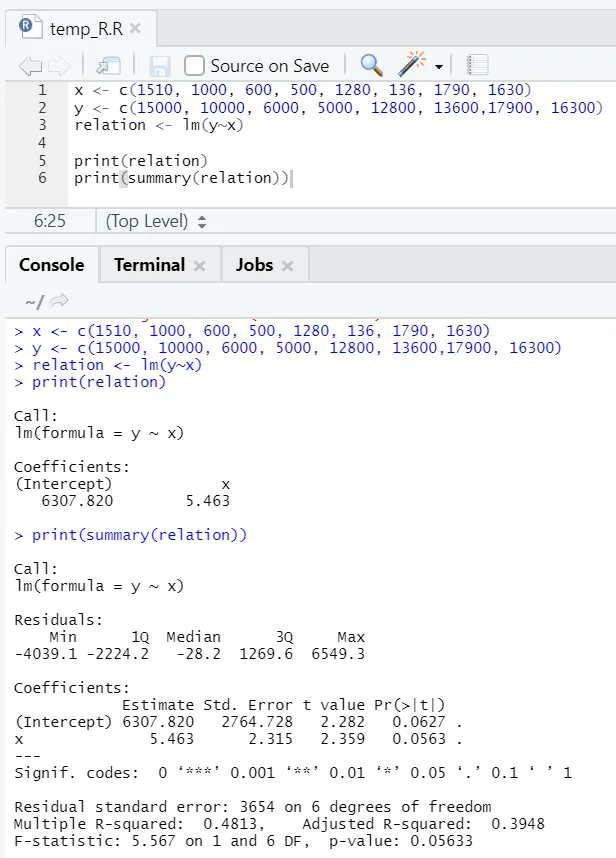
Qui il valore P non è inferiore al 5%. Quindi l'ipotesi nulla non può essere respinta. Non c'è molto significato per dimostrare il rapporto tra la superficie e l'affitto.
Qui il valore del quadrato R è 0, 4813. Ciò implica che solo il 48% della varianza nella variabile di output può essere spiegato dalla variabile di input.
Diciamo ora che dobbiamo prevedere un valore dell'area del pavimento, basato sul modello sopra montato.
Codice R.
x_new <- data.frame(x = 1700)
result <- predict(relation, x_new)
print(result)
Uscita R:
Dopo l'esecuzione del codice R sopra, l'output sarà simile al seguente:
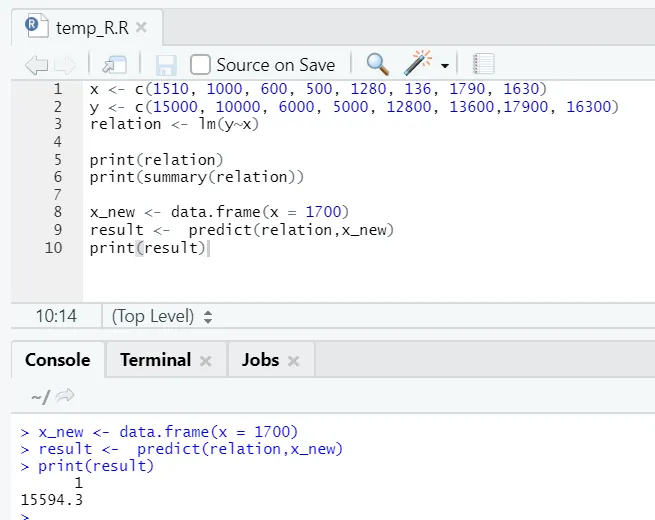
Si può adattarsi e visualizzare la regressione. Ecco il codice R per questo:
# Dai un nome al file grafico png.
png(file = "LinearRegressionSample.png.webp")
# Traccia il grafico.
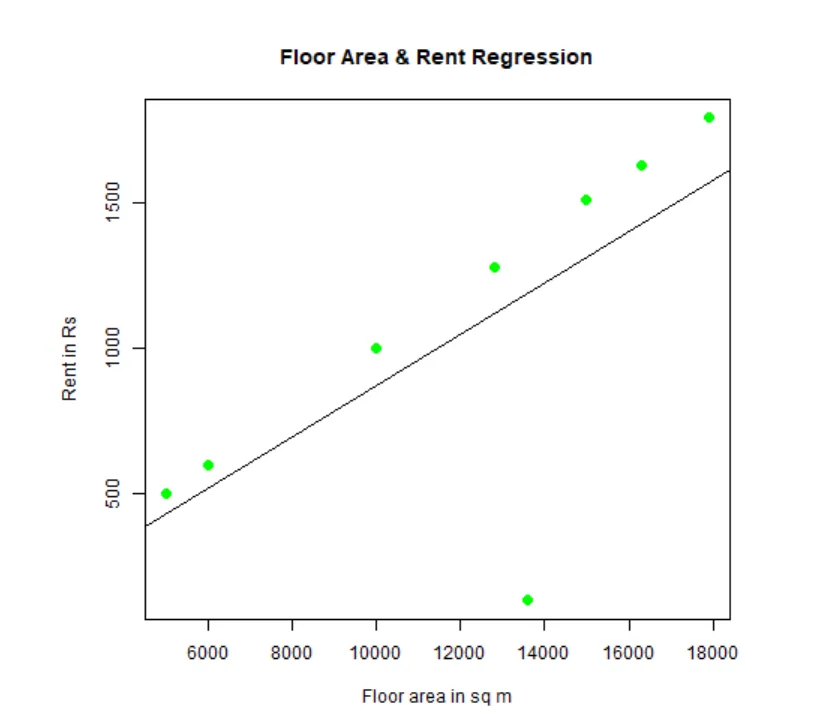
plot(y, x, col = "green", main = "Floor Area & Rent Regression",
abline(lm(x~y)), cex = 1.3, pch = 16, xlab = "Floor area in sq m", ylab = "Rent in Rs")
# Salva il file.
dev.off()
Questo grafico "LinearRegressionSample.png.webp" verrà generato nella directory di lavoro attuale.
g) Test Chi-Square
Questa è una funzione statistica in R. Questo test ha il suo significato per dimostrare se esiste una correlazione tra due variabili categoriali.
Questo test funziona anche come qualsiasi altro test statistico basato sul valore p, si può accettare o rifiutare l'ipotesi nulla.
Sintassi R
chisq.test(data), /code>
Vediamo un esempio pratico di esso.
Codice R.
# Carica la libreria.
library(datasets)
data(iris)
# Crea un frame di dati dal set di dati principale.
iris.data <- data.frame(iris$Sepal.Length, iris$Sepal.Width)
# Crea una tabella con le variabili necessarie.
iris.data = table(iris$Sepal.Length, iris$Sepal.Width)
print(iris.data)
# Eseguire il test Chi-Square.
print(chisq.test(iris.data))
Uscita R:
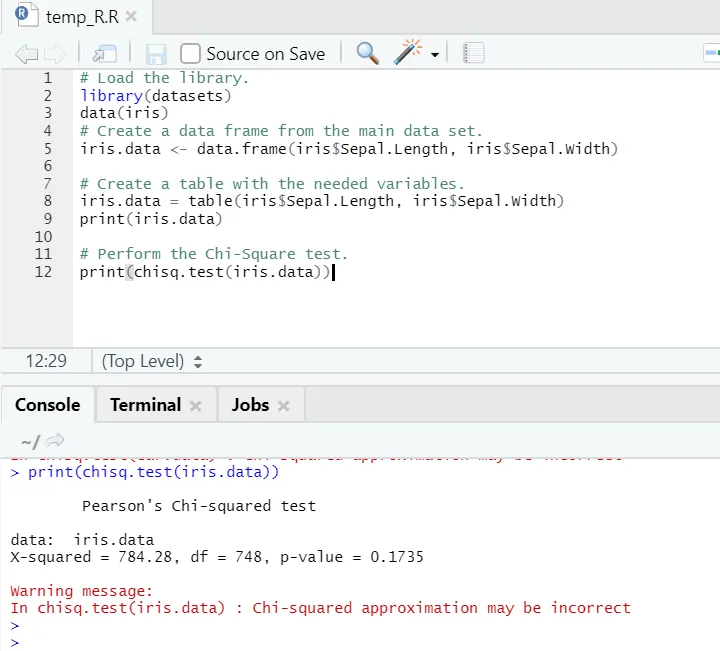
Come si può vedere, il test chi-quadro è stato eseguito su un set di dati dell'iride, considerando le sue due variabili “Sepal. Lunghezza "e" Sepal.Width ".
Il valore p non è inferiore a 0, 05, quindi non esiste correlazione tra queste due variabili. Oppure possiamo dire che queste due variabili non dipendono l'una dall'altra.
Conclusione
Le funzioni in R sono semplici, facili da adattare, facili da comprendere e tuttavia molto potenti. Abbiamo visto una varietà di funzioni che sono usate come parte delle basi in R. Una volta che ci si sente a proprio agio con queste funzioni discusse sopra, si possono esplorare altre varietà di funzioni. Le funzioni ti aiutano a far funzionare il tuo codice in modo semplice e conciso. Le funzioni possono essere integrate o definite dall'utente, tutto dipende dalla necessità mentre si affronta un problema. Le funzioni danno una buona forma a un programma.
Articoli consigliati
Questa è una guida alle funzioni in R. qui discuteremo come scrivere funzioni in R e diversi tipi di funzioni in R con sintassi ed esempi. Puoi anche leggere il seguente articolo per saperne di più -
- Funzioni stringa R
- Funzioni stringa SQL
- Funzioni stringa T-SQL
- Funzioni stringa PostgreSQL