Introduzione al clustering gerarchico
- Recentemente uno dei nostri clienti ha chiesto al nostro team di mettere in evidenza un elenco di segmenti con un ordine di importanza all'interno dei propri clienti per indirizzarli a un franchising di uno dei loro nuovi prodotti lanciati. Chiaramente, la semplice segmentazione dei clienti utilizzando il clustering parziale (k-mean, c-fuzzy) non farà emergere l'ordine di importanza che è qui in cui il clustering gerarchico entra in scena.
- Il clustering gerarchico sta separando i dati in diversi gruppi in base ad alcune misure di somiglianza note come cluster, che essenzialmente mira a costruire la gerarchia tra i cluster. È fondamentalmente un apprendimento senza supervisione e la scelta degli attributi per misurare la somiglianza è specifica dell'applicazione.
Il cluster della gerarchia dei dati
- Clustering agglomerativo
- Clustering Divisivo
Facciamo un esempio di dati, voti ottenuti da 5 studenti per raggrupparli per un prossimo concorso.
| Alunno | votazione |
| UN | 10 |
| B | 7 |
| C | 28 |
| D | 20 |
| E | 35s |
1. Clustering agglomerativo
- Per cominciare, consideriamo ogni singolo punto / elemento qui peso come cluster e continuiamo a fondere i punti / elementi simili per formare un nuovo cluster al nuovo livello fino a quando non restiamo con il singolo cluster è un approccio dal basso verso l'alto.
- Il collegamento singolo e il collegamento completo sono due esempi popolari di raggruppamento agglomerativo. Altro che legame medio e legame centroide. In un unico collegamento, uniamo in ogni passaggio i due cluster, i cui due membri più vicini hanno la distanza minima. Nel collegamento completo, ci uniamo ai membri della distanza più piccola che forniscono la minima distanza massima a coppia.
- Matrice di prossimità, è il nucleo per l'esecuzione del raggruppamento gerarchico, che fornisce la distanza tra ciascuno dei punti.
- Facciamo una matrice di prossimità per i nostri dati riportati nella tabella, poiché stiamo calcolando la distanza tra ciascuno dei punti con altri punti sarà una matrice asimmetrica di forma n × n, nel nostro caso matrici 5 × 5.
Un metodo popolare per i calcoli della distanza sono:
- Distanza euclidea (quadrata)
dist((x, y), (a, b)) = √(x - a)² + (y - b)²
- Distanza di Manhattan
dist((x, y), (a, b)) =|x−c|+|y−d|
La distanza euclidea è più comunemente usata, useremo la stessa qui e andremo con un collegamento complesso.
| Student (cluster) | UN | B | C | D | E |
| UN | 0 | 3 | 18 | 10 | 25 |
| B | 3 | 0 | 21 | 13 | 28 |
| C | 18 | 21 | 0 | 8 | 7 |
| D | 10 | 13 | 8 | 0 | 15 |
| E | 25 | 28 | 7 | 15 | 0 |
Gli elementi diagonali della matrice di prossimità saranno sempre 0, poiché la distanza tra il punto con lo stesso punto sarà sempre 0, quindi gli elementi diagonali sono esenti dalla considerazione per il raggruppamento.
Qui, nell'iterazione 1, la distanza più piccola è 3, quindi uniamo A e B per formare un cluster, formando nuovamente una nuova matrice di prossimità con il cluster (A, B) prendendo il punto del cluster (A, B) come 10, ovvero il massimo di ( 7, 10) così sarebbe la matrice di prossimità di nuova formazione
| Cluster | (A, B) | C | D | E |
| (A, B) | 0 | 18 | 10 | 25 |
| C | 18 | 0 | 8 | 7 |
| D | 10 | 8 | 0 | 15 |
| E | 25 | 7 | 15 | 0 |
Nell'iterazione 2, 7 è la distanza minima, quindi uniamo C ed E formando un nuovo cluster (C, E), ripetiamo il processo seguito nell'iterazione 1 fino a quando non finiamo con il cluster singolo, qui ci fermiamo all'iterazione 4.
L'intero processo è rappresentato nella figura seguente:
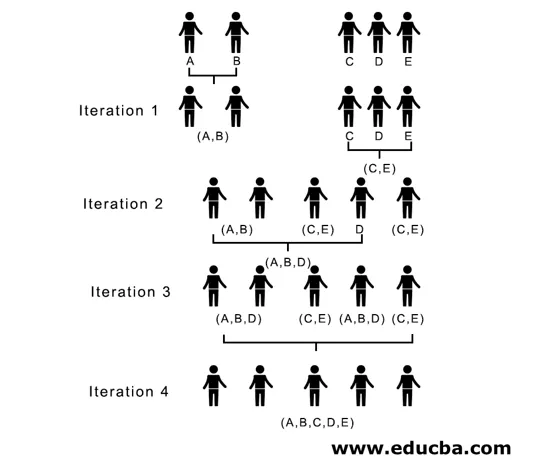
(A, B, D) e (D, E) sono i 2 cluster formati all'iterazione 3, all'ultima iterazione possiamo vedere che siamo rimasti con un singolo cluster.
2. Clustering divisivo
Per cominciare, consideriamo tutti i punti come un singolo cluster e li separiamo dalla distanza più lontana fino a quando non finiamo con singoli punti come singoli cluster (non necessariamente possiamo fermarci nel mezzo, dipende dal numero minimo di elementi che vogliamo in ciascun cluster) ad ogni passo. È esattamente l'opposto del cluster agglomerativo ed è un approccio top-down. Il clustering divisivo è un modo in cui k ripetitivo significa clustering.
La scelta tra Agglomerative e Divisive Clustering dipende nuovamente dall'applicazione, ma alcuni punti da considerare sono:
- Divisivo è più complesso del raggruppamento agglomerativo.
- Il clustering divisivo è più efficiente se non generiamo una gerarchia completa fino ai singoli punti dati.
- Il clustering agglomerativo prende una decisione considerando gli schemi locali, senza tenere conto inizialmente di modelli globali che non possono essere invertiti.
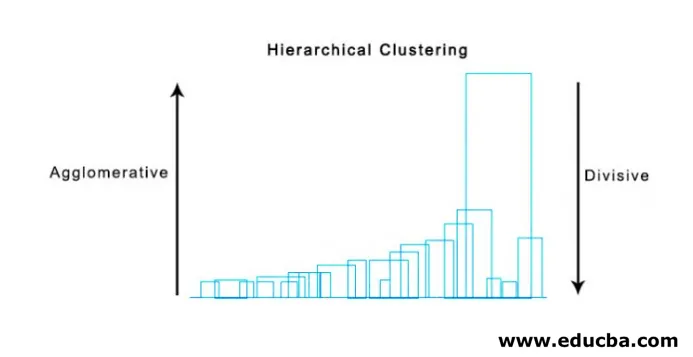
Visualizzazione del clustering gerarchico
Un metodo super utile per visualizzare il clustering gerarchico che aiuta nel mondo degli affari è Dendogram. I dendogrammi sono strutture ad albero che registrano la sequenza di fusioni e divisioni in cui la linea verticale rappresenta la distanza tra i cluster, la distanza tra le linee verticali e la distanza tra i cluster è direttamente proporzionale, cioè più la distanza maggiore è la probabilità che i cluster siano diversi.
Possiamo usare il dendogramma per decidere il numero di cluster, basta tracciare una linea che si interseca con una linea verticale più lunga sul dendogramma, un numero di linee verticali intersecate sarà il numero di cluster da considerare.
Di seguito è riportato l'esempio Dendogramma.
Esistono pacchetti Python piuttosto semplici e diretti ed è funzioni per eseguire cluster gerarchici e tracciare dendogrammi.
- La gerarchia di scipy.
- Cluster.hierarchy.dendogram per la visualizzazione.
Scenari comuni in cui viene utilizzato il cluster gerarchico
- Segmentazione del cliente nel marketing di prodotti o servizi.
- Pianificazione urbana per identificare i luoghi per costruire strutture / servizi / edifici.
- Social Network Analysis, ad esempio, identifica tutti i fan di MS Dhoni per pubblicizzare il suo film biografico.
Vantaggi del clustering gerarchico
I vantaggi sono stati indicati di seguito:
- Nel caso di clustering parziale come k-medie, il numero di cluster dovrebbe essere noto prima del clustering, il che non è possibile nelle applicazioni pratiche, mentre nel clustering gerarchico non è richiesta alcuna conoscenza preliminare del numero di cluster.
- Il clustering gerarchico genera una gerarchia, ovvero una struttura più informativa rispetto all'insieme non strutturato dei cluster flat restituiti dal clustering parziale.
- Il clustering gerarchico è facile da implementare.
- Mostra i risultati nella maggior parte degli scenari.
Conclusione
Il tipo di clustering fa la differenza quando vengono presentati i dati, essendo il cluster gerarchico più informativo e facile da analizzare è più preferito del cluster parziale. Ed è spesso associato a mappe di calore. Per non dimenticare gli attributi scelti per calcolare la somiglianza o la dissomiglianza influenza principalmente sia i cluster che la gerarchia.
Articoli consigliati
Questa è una guida al Clustering Gerarchico. Qui discutiamo dell'introduzione, dei vantaggi del Clustering gerarchico e degli scenari comuni in cui viene utilizzato il Clustering gerarchico. Puoi anche consultare i nostri altri articoli suggeriti per saperne di più–
- Algoritmo di clustering
- Clustering in Machine Learning
- Clustering gerarchico in R
- Metodi di clustering
- Come rimuovere la gerarchia nel tableau?