
Introduzione all'ordinamento degli algoritmi in JavaScript
Simile alla maggior parte degli altri linguaggi di programmazione, è possibile imbattersi in scenari in cui è necessario ordinare alcuni numeri in JavaScript in ordine crescente o decrescente. Per farlo, possiamo usare molti algoritmi come Bubble sort, Selection Sort, Merge sort, Quicksort, ecc. Questi algoritmi non solo differiscono nel modo in cui funzionano, ma ognuno ha le sue diverse esigenze in termini di memoria e tempo, approfondisci alcuni dei più importanti algoritmi di ordinamento e scopri come utilizzarli nel tuo codice JavaScript.
Primi 6 algoritmi di ordinamento in JavaScript
Ecco alcuni algoritmi di ordinamento in JavaScript spiegati di seguito con esempi:
1. Algoritmo di ordinamento delle bolle
Considerato uno degli strumenti più comuni di questo commercio, l'ordinamento a bolle funziona creando un ciclo che confronta ogni elemento dell'array con un altro elemento. Se l'elemento confrontato è più piccolo di quello a portata di mano, cambiamo posto. Questo continua fino a quando non abbiamo un passaggio in cui nessun oggetto nell'array è più grande di quello accanto.
Bubble Sort ha complessità temporale O (n 2 ) e complessità spaziale O (n).
Codice:
function swap(arr, firstIndex, secondIndex)(
var temp = arr(firstIndex);
arr(firstIndex) = arr(secondIndex);
arr(secondIndex) = temp;
)
function bubbleSortAlgo(arraaytest)(
var len = arraaytest.length,
i, j, stop;
for (i=0; i < len; i++)(
for (j=0, stop=len-i; j < stop; j++)(
if (arraaytest(j) > arraaytest(j+1))(
swap(arraaytest, j, j+1);
)
)
)return arraaytest;
)
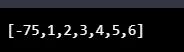
console.log(bubbleSortAlgo((3, 6, 2, 5, -75, 4, 1)));
Produzione:
2. Algoritmo di ordinamento della selezione
Ora che abbiamo finito di discutere l'algoritmo di ordinamento a bolle, diamo un'occhiata proprio come un algoritmo popolare per l'ordinamento chiamato ordinamento per selezione.
A differenza di Bubble Sort, ci concentriamo sulla ricerca del valore più piccolo nell'array per eseguire l'ordinamento. Ecco una descrizione dettagliata di come funziona l'ordinamento per selezione:
- Supponiamo che il primo elemento dell'array sia il più piccolo.
- Confrontiamo questo articolo con quello successivo nella matrice.
- Se l'elemento successivo è più piccolo di quello a portata di mano, impostiamo l'elemento successivo come nuovo valore più piccolo.
- Continuiamo a ripetere questi passaggi fino a raggiungere la fine dell'array.
- Quando troviamo un valore nell'array che è più piccolo di quello con cui abbiamo iniziato, scambiamo le loro posizioni.
- Continuiamo a fare i confronti e passiamo all'elemento successivo. Fino a quando l'intero array non viene ordinato.
Proprio come l'algoritmo Bubble Sort, l'ordinamento Selection ha complessità temporale O (n 2 ) e complessità spaziale O (n).
Codice:
function SelectionSortAlgo(array, compare_Function) (
function comp(a, b) (
return a - b;
)
var min = 0;
var index = 0;
var temp = 0;
compare_Function = compare_Function || compare;
for (var i = 0; i < array.length; i += 1) (
index = i;
min = array(i);
for (var j = i + 1; j < array.length; j += 1) (
if (compare_Function(min, array(j)) > 0) (
min = array(j);
index = j;
)
)
temp = array(i);
array(i) = min;
array(index) = temp;
)
return array;
)
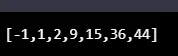
console.log(SelectionSortAlgo((9, 15, 2, 44, -1, 36, 1), function(a, b) ( return a - b; )));
Produzione:
3. Unisci algoritmo di ordinamento
Simile a Bubble Sort e Selection Sort, Merge sort è uno dei più diffusi algoritmi di ordinamento nell'informatica, è possibile implementarlo nella maggior parte dei linguaggi di programmazione e ha buone prestazioni senza essere troppo bisognoso di risorse.
Unisci ordinamento utilizza il metodo Dividi e conquista per ordinare un array o qualsiasi elenco di elementi. Il termine divide e conquista significa che dividiamo un grosso problema in diversi problemi minori e quindi risolviamo questi piccoli problemi. Una volta risolti i problemi minori, uniamo i risultati che risultano nella soluzione al grande problema.
Comprendere l'algoritmo è semplice in realtà:
- Dividiamo l'array dato in n array ciascuno di questi array contiene solo 1 elemento.
- Unire gli array per produrre un nuovo array.
- Ripetere il passaggio 2 fino a quando rimane solo 1 array, che sarà l'array ordinato.
Codice:
function merge_sort_algo(left, right)
(
var i = 0;
var j = 0;
var result = ();
while (i < left.length || j < right.length) (
if (i === left.length) (
// j is the only index left_part
result.push(right(j));
j++;
)
else if (j === right.length || left(i) <= right(j)) (
result.push(left(i));
i++;
) else (
result.push(right(j));
j++;
)
)
return result;
)
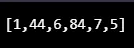
console.log(merge_sort_algo((1, 44, 6), (84, 7, 5)));
Produzione:
4. Algoritmo di ordinamento rapido
Quicksort è uno dei modi più efficienti per ordinare gli elementi nei sistemi informatici. Simile a unire l'ordinamento, Quicksort lavora sull'algoritmo di divisione e conquista. In questo, troviamo un articolo pivot nell'array per confrontare tutti gli altri array di elementi e quindi spostiamo gli articoli in un modo in cui tutti gli elementi prima dei nostri articoli pivot selezionati sono più piccoli e tutti gli articoli dopo l'elemento pivot hanno dimensioni maggiori. Una volta che lo abbiamo fatto, la chiave è continuare a farlo ripetutamente e avremo il nostro array ordinato.
Di seguito sono riportati i passaggi che è possibile seguire per implementare l'algoritmo quicksort:
- Selezioniamo un elemento dell'array e lo chiamiamo "Punto di articolazione"
- Iniziamo un puntatore chiamato puntatore di sinistra dal quale si trova il primo elemento dell'array.
- Allo stesso modo, iniziamo un puntatore chiamato il puntatore giusto all'ultimo elemento dell'array.
- Se il valore dell'elemento nel puntatore a sinistra è inferiore rispetto al punto pivot selezionato, spostiamo il puntatore a sinistra verso sinistra (aggiungi +1 ad esso) e continuiamo a ripeterlo fino a quando il valore nel puntatore a sinistra non risulta più grande del valore del punto pivot o uguale ad esso.
- Se il valore dell'elemento sul puntatore destro nell'elenco è superiore al valore dell'elemento pivot, modifichiamo il puntatore destro a sinistra. Ripetere l'operazione fino a quando il valore sul puntatore a destra non è inferiore (o uguale a) al valore di pivot.
- Quando il valore del puntatore a sinistra è inferiore o uguale al valore del puntatore a destra, scambiare i valori.
- Sposta il puntatore destro a sinistra di uno, il puntatore sinistro a destra di uno.
- Ripetere fino a quando i puntatori sinistro e destro si incontrano.
Codice:
function quickSortAlgo(origArray) (
if (origArray.length <= 1) (
return origArray;
) else (
var left = ();
var right = ();
var newArray = ();
var pivot = origArray.pop();
var length = origArray.length;
for (var i = 0; i < length; i++) (
if (origArray(i) <= pivot) (
left.push(origArray(i));
) else (
right.push(origArray(i));
)
)
return newArray.concat(quickSortAlgo(left), pivot, quickSortAlgo(right));
)
)
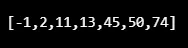
var myArray = (13, 50, 2, 45, -1, 74, 11 );
var arreySorted = quickSortAlgo(myArray);
console.log(arreySorted);
Produzione:
5. Algoritmo di ordinamento per inserzione
Per quanto riguarda la facilità di implementazione, l'ordinamento per inserzione è ampiamente noto come uno degli algoritmi più semplici. In Insertion Sort, gli elementi dell'array vengono confrontati tra loro e quindi disposti in un ordine particolare. Questo è molto simile alla disposizione delle carte in un mazzo. L'ordinamento di inserimento del nome deriva dal processo di selezione di un elemento e inserimento nella posizione corretta, quindi ripetizione per tutti gli elementi.
Ecco come funziona l'algoritmo:
- Il primo elemento dell'array è considerato già ordinato.
- Scegli l'elemento successivo dell'array.
- Confronta l'elemento selezionato con tutti gli elementi dell'array.
- Sposta ogni elemento dell'array che è maggiore del valore dell'elemento selezionato.
- Inserisci l'elemento
- Ripetere i passaggi da 2 a 5 fino a quando l'array non viene ordinato.
Codice:
function insertion_Sort_algo(arr)
(
for (var i = 1; i < arr.length; i++)
(
if (arr(i) < arr(0))
(
arr.unshift(arr.splice(i, 1)(0));
)
else if (arr(i) > arr(i-1))
(
continue;
)
else (
for (var j = 1; j < i; j++) (
if (arr(i) > arr(j-1) && arr(i) < arr(j))
(
arr.splice(j, 0, arr.splice(i, 1)(0));
)
)
)
)
return arr;
)
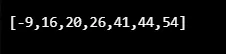
console.log(insertion_Sort_algo((44, 20, 26, 54, -9, 41, 16)));
Produzione:
6. Algoritmo di ordinamento dell'heap
L'ordinamento degli heap è un modo di ordinare gli elementi utilizzando la struttura dati "Heap". Il metodo è abbastanza simile alla tecnica di ordinamento della selezione discussa in precedenza. Ora ti starai chiedendo di Heaps e come sono definiti, prima di arrivare all'algoritmo, capiamo prima gli heap.
In poche parole, un heap è un albero binario con alcune regole aggiunte. Una regola afferma che in heap, l'albero deve essere un albero binario completo, il che significa semplicemente che è necessario riempire tutti i nodi del livello corrente prima di aggiungerne un altro. La regola successiva per l'heap è che ci deve essere una relazione figlio e padre definita con i valori dell'elemento dell'heap.
In un min-heap, il valore di un genitore deve essere inferiore ai suoi figli. In un heap massimo, come puoi immaginare, il valore di un genitore deve essere maggiore del suo figlio.
Ora che le definizioni sono fuori mano, diamo un'occhiata a come funziona heapsort:
- Per prima cosa creiamo un heap massimo che assicuri che l'elemento di valore più alto sia in alto.
- Cambiamo l'elemento superiore con l'ultimo elemento dell'heap e rimuoviamo l'elemento superiore dall'heap e lo memorizziamo in un array ordinato.
- Continuiamo a ripetere i passaggi uno e due finché non rimane un solo elemento nell'heap.
Una cosa da tenere a mente è che gli Heaps non sono supportati nativamente in JavaScript, quindi dobbiamo ricorrere all'implementazione degli Heaps usando gli array. La complessità spaziale dell'heap sort è O (1) che è eccellente e mentre è un po 'più complicato rispetto all'unione dell'ordinamento o dell'inserzione quando si tratta di comprensione e implementazione, penso che per i vantaggi in termini di prestazioni, alla fine è meglio usare in grandi progetti.
Codice:
var arrLength;
function heapRoot(input, i) (
var left = 2 * i + 1;
var right = 2 * i + 2;
var max = i;
if (left input(max)) (
max = left;
)
if (right input(max)) (
max = right;
)
if (max != i) (
swap(input, i, max);
heapRoot(input, max);
)
)
function swap(input, index_A, index_B) (
var temp = input(index_A);
input(index_A) = input(index_B);
input(index_B) = temp;
)
function heapSortAlgo(input) (
arrLength = input.length;
for (var i = Math.floor(arrLength / 2); i >= 0; i -= 1) (
heapRoot(input, i);
)
for (i = input.length - 1; i > 0; i--) (
swap(input, 0, i);
arrLength--;
heapRoot(input, 0);
)
)
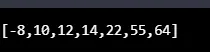
var arr = (12, 10, 22, 55, -8, 64, 14);
heapSortAlgo(arr);
console.log(arr);
Produzione:
Conclusione
L'ordinamento è una parte importante della creazione di applicazioni e siti Web con JavaScript. Ora che hai familiarità con alcuni degli algoritmi più importanti per svolgere il lavoro, dovresti sentirti più sicuro in JS Development.
Un fatto importante da tenere a mente sui vari ordinamenti è che non devi davvero preoccuparti troppo di quale algoritmo usare nella maggior parte dei casi. Ora che l'hardware del computer è così potente, i moderni processori per telefono e desktop non possono sudare nell'ordinare anche centinaia di elementi in pochi millisecondi. Sono solo i casi in cui sei bloccato con hardware lento o situazioni in cui riesci a ottimizzare ogni singola sezione di codice in cui cambiare gli algoritmi di ordinamento può essere utile.
Articoli consigliati
Questa è una guida per ordinare gli algoritmi in JavaScript. Qui discutiamo i 6 migliori algoritmi di ordinamento in JavaScript insieme ad esempi e implementazione del codice. Puoi anche consultare i seguenti articoli per saperne di più -
- Compilatori JavaScript
- Invertire in JavaScript
- Introduzione a JavaScript
- Quadrati in Java
- Algoritmi di ordinamento rapido in Java
- Matrici nella struttura dei dati
- Algoritmo C ++ | Esempi di algoritmo C ++