Introduzione all'algoritmo di cluster gerarchico
L'algoritmo di clustering gerarchico è una tecnica di Machine Learning senza supervisione. Ha lo scopo di trovare un raggruppamento naturale basato sulle caratteristiche dei dati.
L'algoritmo di clustering gerarchico mira a trovare gruppi nidificati dei dati creando la gerarchia. È simile alla tassonomia biologica della pianta o del regno animale. I cluster gerarchici sono generalmente rappresentati usando l'albero gerarchico noto come dendrogramma.
Tipi di algoritmo di clustering gerarchico
Gli algoritmi di clustering gerarchico sono di 2 tipi:
- divisive
- agglomerante
1. Divisivo
Questo è un approccio dall'alto verso il basso, in cui inizialmente considera tutti i dati come un unico gruppo, quindi suddivide iterativamente i dati in sottogruppi. Se è noto il numero di un algoritmo di clustering gerarchico, il processo di divisione si interrompe una volta raggiunto il numero di cluster. Altrimenti, il processo si interrompe quando i dati non possono essere più suddivisi, il che significa che il sottogruppo ottenuto dall'iterazione corrente è lo stesso di quello ottenuto dall'iterazione precedente (si può anche considerare che la divisione si interrompe quando ogni punto di dati è un cluster ).
2. Agglomerativo
È un approccio dal basso che si basa sulla fusione di cluster. Inizialmente, i dati sono divisi in m cluster singleton (dove il valore di m è il numero di campioni / punti dati). Due cluster vengono uniti in uno iterativo, riducendo così il numero di cluster in ogni iterazione. Questo processo di fusione dei cluster si interrompe quando tutti i cluster sono stati uniti in uno o viene raggiunto il numero di cluster desiderati.
Al livello 1, ci sono m cluster che vengono ridotti a 1 cluster al livello m. I punti dati che vengono uniti per formare un cluster a un livello inferiore rimangono nello stesso cluster anche ai livelli più alti. Ad esempio, supponiamo che ci siano 8 punti x1..x8, quindi inizialmente ci sono 8 cluster al livello 1. Supponiamo che i punti x1 e x2 vengano uniti in un cluster al livello 2, quindi fino al livello 8, rimangono nello stesso cluster.
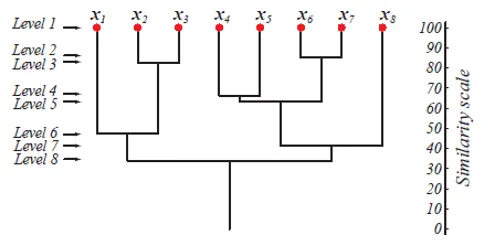
La figura sopra mostra una rappresentazione dendrografica dell'approccio di raggruppamento di agglomerati per 8 punti dati e la scala di somiglianza corrispondente a ciascun livello.
I livelli dei cluster ci danno un'idea di quanto siano simili i punti dati nei cluster. Come mostrato nella figura 1, prima i punti dati vengono uniti in un cluster, simili sono. Pertanto, i punti di dati all'interno di un cluster a livello 2 (ad es. X2 e x3) sono più simili di quei punti di dati in un cluster a livello 6 (ad es. X1 e x2).
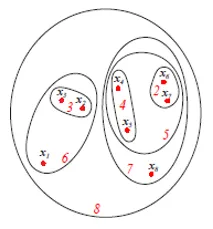
La figura sopra mostra la rappresentazione del diagramma Set o Venn dell'approccio di raggruppamento agglomerativo degli 8 punti dati sopra menzionati. Sia i dendrogrammi che le rappresentazioni dei set possono essere utilizzati per il clustering. Tuttavia, un dendrogramma è di solito preferibile che la rappresentazione patrimoniale non possa rappresentare quantitativamente le somiglianze tra i cluster.
Passaggi per l'algoritmo di cluster gerarchico
Seguiamo i seguenti passaggi per l'algoritmo di clustering gerarchico che sono riportati di seguito:
1. Algoritmo
Algoritmo di clustering gerarchico agglomerativo
- Inizia a inizializzare c, c1 = n, Di = (xi), i = 1, …, n '
- Esegui c1 = c1 - 1
- Trova i cluster più vicini, ad esempio Di e Dj
- Unisci Di e Dj
- Fino a c = c1
- Restituisce i cluster c
- Fine
Questo algoritmo inizia inizialmente con n cluster in cui ciascun punto dati è un cluster. Ad ogni iterazione, il numero di cluster si riduce di 1 man mano che i 2 cluster più vicini vengono uniti. Questo processo continua fino a quando il numero di cluster si riduce al valore predefinito c.
Come decidere quali cluster sono vicini?
Ciò viene definito utilizzando diverse metriche di distanza che sono le seguenti:
- La distanza minima tra i cluster dmin (Di, Dj). Utile per single.
- La distanza massima tra i cluster dmax (Di, Dj). Utile per completo.
- La distanza media tra i cluster davg (Di, Dj).
Che cos'è il collegamento singolo e il collegamento completo?
- Quando dmin (di, dj) viene utilizzato per trovare la distanza tra due cluster e l'algoritmo termina se la distanza tra i cluster più vicini supera una soglia, l'algoritmo viene chiamato un singolo algoritmo di collegamento.
- Quando dmax (Di, Dj) viene utilizzato per trovare la distanza tra due cluster e l'algoritmo termina se la distanza tra i cluster più vicini supera una soglia, l'algoritmo viene chiamato algoritmo di collegamento completo.
- Consideriamo ogni punto dati come un nodo di un grafico. C'è un vantaggio tra due punti dati se appartengono allo stesso cluster. Quando vengono uniti due cluster più vicini, viene aggiunto un bordo. Si chiama un singolo collegamento perché esiste un percorso univoco da un nodo all'altro.
- L'algoritmo di collegamento completo unisce due cluster minimizzando la distanza tra i due punti più lontani.
- Un singolo algoritmo di collegamento genera un albero di spanning. Tuttavia, questo algoritmo è suscettibile al rumore. Un algoritmo di collegamento completo genera un grafico completo.
Qual è la complessità temporale dell'algoritmo?
Supponiamo di avere n modelli nello spazio d-dimensionale e di usare dmin (Di, Dj) per formare cluster c. Dobbiamo calcolare n (n - 1) distanze tra punti - ognuna delle quali è un calcolo O (d 2 ) - e posizionare i risultati in una tabella di distanza tra punti. La complessità dello spazio è O (n 2 ). Per trovare la coppia di distanza minima (per la prima fusione) è necessario scorrere l'elenco completo, mantenendo l'indice della distanza minima.
Pertanto, per il primo passaggio agglomerativo, la complessità è O (n (n - 1) (d 2 + 1)) = O (n 2 d 2 ). Per un'altra fase di agglomerazione arbitraria (ovvero da c1 a c1 - 1), passiamo semplicemente attraverso le distanze "non utilizzate" di n (n - 1) - c1 nella lista e troviamo la più piccola per cui x e x 'si trovano in diversi cluster . Questo è, di nuovo, O (n (n − 1) −c1). La complessità temporale totale è quindi O (cn 2 d 2 ) e in condizioni tipiche n >> c.
2. Visualizzazione
Una volta divisi i dati in cluster, è buona norma visualizzare i cluster in modo da avere un'idea di come appare il raggruppamento. Ma visualizzare questi dati ad alta dimensione è difficile. Quindi usiamo Principal Component Analysis (PCA) per la visualizzazione. Dopo la PCA, otteniamo i punti dati nello spazio dimensionale basso (generalmente 2D o 3D) che possiamo tracciare per vedere il raggruppamento.
Nota: dimensione elevata indica un numero elevato di funzioni e non un numero di punti dati.3. Valutazione
Uno dei metodi per la valutazione dei cluster è che la distanza dei punti tra i cluster (distanza tra cluster) dovrebbe essere molto maggiore della distanza dei punti all'interno del cluster (distanza intracluster).
Conclusione
Di seguito sono riportati i pochi takeaway chiave:
- L'algoritmo di clustering gerarchico viene utilizzato per trovare modelli nidificati nei dati
- Il clustering gerarchico è di 2 tipi: Divisive e Agglomerative
- Dendrogram e set / Venn diagram possono essere usati per la rappresentazione
- Il collegamento singolo unisce due cluster riducendo al minimo la distanza minima tra di loro. Forma uno spanning
- Il collegamento completo unisce due cluster riducendo al minimo la distanza massima tra i due forma un grafico completo.
- La complessità temporale totale dell'algoritmo di clustering gerarchico è O (cn 2 d 2 ), dove c è il numero predefinito di cluster, n è il numero di pattern e d è lo spazio d-dimensionale degli n pattern.
Articoli consigliati
Questa è una guida all'algoritmo di clustering gerarchico. Qui discutiamo i tipi e i passaggi degli algoritmi di clustering gerarchico. Puoi anche consultare i seguenti articoli per saperne di più-
- Analisi gerarchica del clustering
- Clustering gerarchico in R '
- Algoritmo di clustering
- Che cos'è il clustering nel data mining?
- Clustering gerarchico Clustering agglomerativo e divisivo
- Algoritmo C ++ | Esempi di algoritmo C ++