
Introduzione alla serie Fibonacci in Python
Serie di Fibonacci in Python, questa è indicata come una serie di numeri, in cui il numero successivo è la somma dei due numeri presenti.
Per esempio:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 ..so on
Quindi qui 0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8+ 13 = 21 e così via.
Guardando quanto sopra, si avrebbe una certa idea di cosa stiamo parlando.
Tuttavia, in termini di regola matematica, può essere scritto come:

Dove l'ennesimo numero è la somma del numero in corrispondenza dei punti (n-1) e (n-2). Quando si tratta di implementare la serie Fibonacci, potrebbero esserci un certo numero di linguaggi di codifica attraverso i quali potrebbe essere fatto.
Tuttavia, Python è un linguaggio ampiamente utilizzato al giorno d'oggi. Vediamo l'implementazione della serie Fibonacci attraverso Python. Si dovrebbe essere consapevoli delle istruzioni di condizionamento di base come loop, if-else, while loop, ecc. In Python, prima di procedere qui. Altrimenti, sarebbe bello se si potesse rivederlo e poi riprendere il contenuto in arrivo. Qui a scopo dimostrativo, sto usando spyder che è IDE per il linguaggio di programmazione Python. Si può usare qualsiasi altro notebook IDE o Ipython anche per l'esecuzione dei programmi Python.
Serie Fibonacci in Python
Vediamo l'implementazione del numero e della serie di Fibonacci considerando che 1 ° due elementi di Fibonacci sono 0 e 1:
Tuttavia, puoi modificare la funzione di Fibonacci secondo le tue esigenze, ma vedi prima le basi e passa gradualmente agli altri.
Codice Python per trovare l'ennesimo numero di Fibonacci
Codice 1:
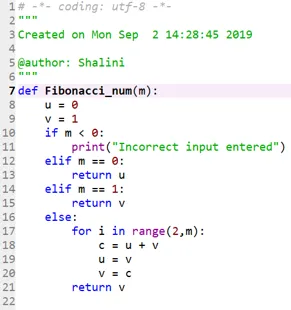
def Fibonacci_num(m):
u = 0
v = 1
if m < 0:
print("Incorrect input entered")
elif m == 0:
return u
elif m == 1:
return v
else:
for i in range(2, m):
c = u + v
u = v
v = c
return v
Codice 2:
Produzione:
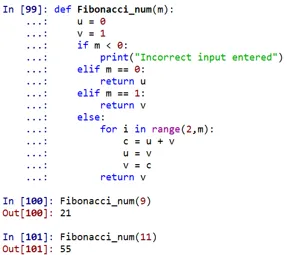
Come si può vedere, il numero di Fibonacci al 9 ° posto sarebbe 21, e all'11 ° posto sarebbe 55.
- Qui "fibonacci_num" è una funzione definita, che si occupa di trovare il numero di Fibonacci con l'aiuto di determinate condizioni. Questa funzione può essere richiamata specificando qualsiasi posizione.
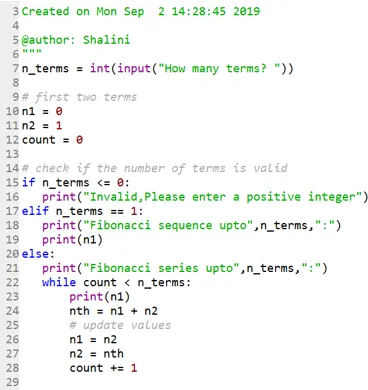
Ora vediamo come si possono stampare le serie fino alla posizione menzionata:
Codice:
Produzione:
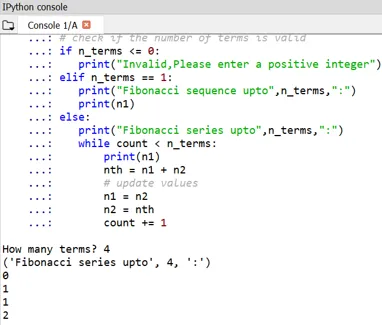
Si può notare che l'inizio dei numeri di Fibonacci è definito come 0 e 1.
- Se qualcuno vuole definire i propri termini iniziali, ciò può essere fatto allo stesso modo modificando n1 e n2. Ecco l'esempio per questo:
Diciamo ora che vogliamo che i nostri termini di partenza siano: n1 = 3, n2 = 5
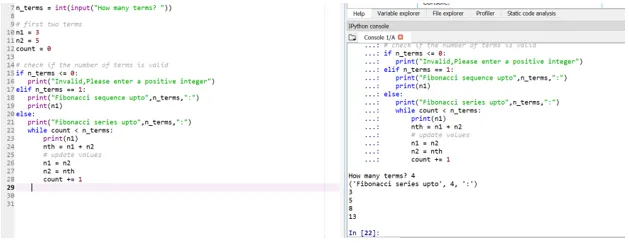
Quindi qui la tua posizione al 4 ° termine (viene preso l'input dell'utente), sarà decisa in base ai termini di partenza.
Metodi attraverso i quali è possibile generare la serie Fibonacci
Di seguito sono riportati i tre metodi, attraverso i quali è possibile generare le serie di Fibonacci:
1. Attraverso i generatori
Codice:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
Produzione:
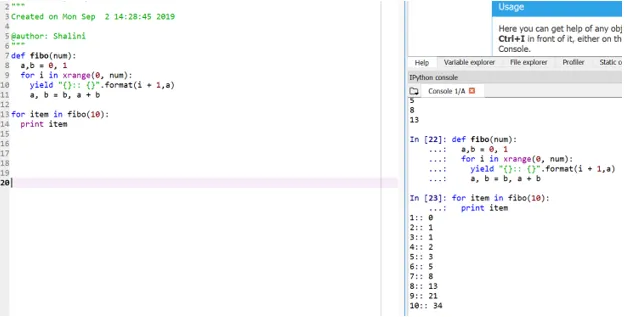
Questo metodo viene chiamato "generatore" perché la funzione xrange è un generatore di numeri compresi tra 0 e num e yield è il generatore di output formattato.
Ecco cosa fa xrange per te:

Qui la serie Fibonacci è stata definita sotto forma di funzione, all'interno della quale per la funzione loop, xrange e yield si occupa dell'output.
2. Attraverso per il ciclo
Codice:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
Produzione:

Come si può vedere, è stato usato simple for loop, per stampare la serie di Fibonacci tra 0 e 10. All'interno di loop, sono stati assegnati nuovi valori alle variabili. U e v sono i valori iniziali predefiniti di Fibonacci che sono stati impostati rispettivamente su 0 e 1.
Per quanto riguarda l'esecuzione del ciclo, il nuovo valore u è il vecchio valore v, mentre il nuovo valore v è la somma dei vecchi valori di u v. Questo continua fino alla fine dei valori dell'intervallo.
3. Attraverso la ricorsione
Codice:
#Through recursion
def fibonacci_ser(m):
if(m <= 1):
return m
else:
return(fibonacci_ser(m-1) + fibonacci_ser(m-2))
m = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(m):
print fibonacci_ser(i),
Produzione:
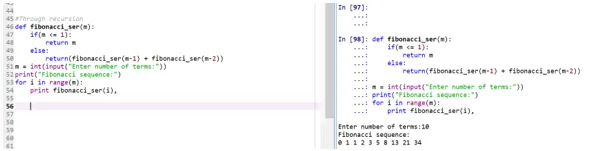
- La funzione "fibonacci_ser" sta chiamando a se stessa per stampare la serie Fibonacci.
- E quindi il metodo ha preso il nome di "ricorsione".
Passaggi seguiti qui:
- Qui è stato chiesto all'utente di inserire il luogo in cui deve essere stampata la serie Fibonacci.
- Il numero passa attraverso la funzione "fibonacci_ser".
- La condizione viene verificata, se la lunghezza fornita è inferiore a 1 o meno. Se sì, il risultato è dato immediatamente.
- Tuttavia, se la lunghezza è maggiore di 1, vengono fatte chiamate ricorsive a "fibonacci_ser" con argomenti di lunghezza inferiore a 1 e 2, ovvero fibonacci_ser (m-1) e fibonacci_ser (m-2).
- Quindi, la ricorsione fornisce l'output desiderato e lo stampa.
- Quindi, in breve, abbiamo discusso di tre modi per mostrare la serie di Fibonacci.
- Attraverso per ciclo, attraverso generatori e attraverso la ricorsione.
Tutti e tre i codici Python sono riassunti
Di seguito sono riportati i tre codici Python:
1. Attraverso i generatori
Codice:
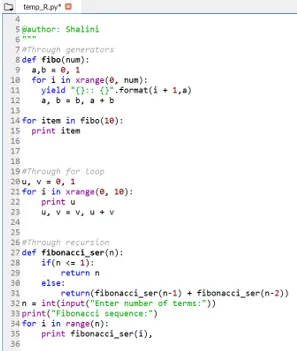
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
2. Attraverso per il ciclo
Codice:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
3. Attraverso la ricorsione
Codice:
def fibonacci_ser(n):
if(n <= 1):
return n
else:
return(fibonacci_ser(n-1) + fibonacci_ser(n-2))
n = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(n):
print fibonacci_ser(i),
Riassumendo sopra sono tutte le procedure, bisogna esercitarsi per avere una buona presa su tutti.
Produzione:
Conclusione
Passando attraverso il contenuto sopra di Fibonacci, si avrebbe una comprensione cristallina dei numeri e delle serie di Fibonacci, specializzati con il pitone. Una volta, ci si sente a proprio agio con la logica della serie Fibonacci, generare un altro set di serie, lavorare con altri numeri e con vari metodi sarà ora un gioco da ragazzi per te. Un approccio logico è l'unico modo per eccellere in questo.
Articoli consigliati
Questa è una guida alla serie Fibonacci in Python. Qui discutiamo di numeri e serie di Fibonacci, specializzati con Python, generando un altro set di serie, lavorando con altri numeri e con vari metodi. Puoi anche consultare i nostri altri articoli correlati per saperne di più -
- Generatore di numeri casuali in Python
- Funzioni matematiche in Python
- Fattoriale in Python
- Incapsulamento in Python
- Serie Fibonacci in Java
- Funzionalità di Python
- Programma fattoriale in JavaScript
- Generatore di numeri casuali in Matlab
- Generatore di numeri casuali in C #
- Incapsulamento in JavaScript