
Introduzione alla funzione ricorsiva in Java
Una funzione ricorsiva è quella che si chiama una o più volte. Una funzione ricorsiva viene utilizzata in situazioni in cui è necessario eseguire ripetutamente lo stesso insieme di operazioni fino al raggiungimento del risultato. Esegue diverse iterazioni e l'istruzione del problema diventa sempre più semplice con ogni iterazione.
È sempre necessario specificare un limite di base durante la scrittura di una funzione ricorsiva, altrimenti si verifica un errore di overflow dello stack. Uno stack è un'area di memoria riservata per mantenere le invocazioni del metodo. L'errore è dovuto al fatto che la funzione inizia l'esecuzione continua poiché non sarà in grado di trovare la condizione limite e quindi esaurire la memoria allocata. Quindi, per evitare lo Stack Overflow, definiamo determinate condizioni di base con l'aiuto delle istruzioni "if … else" (o di qualsiasi altra istruzione condizionale) che fa arrestare la funzione di ricorsione non appena viene completato il calcolo richiesto.
Tipi di ricorsione in Java
Esistono 2 tipi di ricorsione in Java. Loro sono:
1. Ricorsione diretta
Sintassi:
Qui la funzione1 si chiama continuamente, quindi è una funzione ricorsiva.
public static void main(String() args)(
//few lines of code
function();
//few lines of code
)
function() (
//few lines of code
function();
//few lines of code
)
Esempio
Il fattoriale di un numero è un esempio di ricorsione diretta. Il principio di base della ricorsione è quello di risolvere un problema complesso suddividendolo in quelli più piccoli. Ad esempio, nel caso del fattoriale di un numero calcoliamo il fattoriale di "i" se ne conosciamo il fattoriale di "i-1".
Codice:
public class Factorial (
static int fact(int i)(
if (i == 1)
return 1;
else
return(i * fact(i-1));
)
public static void main(String() args) (
System.out.println("The factorial of given number 6 is: "+fact(6));
)
)
Produzione:

2. Ricorsione indiretta / reciproca
Una funzione1 che chiama un'altra funzione2, che a sua volta chiama la funzione1 direttamente o indirettamente, è chiamata funzione ricorsiva indiretta.
Sintassi:
Considera 2 funzioni chiamate function1 () e function2 (). Qui function1 chiama function2 e function2 chiama function1.
function1()(
//few lines of code
function2();
//few lines of code
)
function2()(
//few lines of code
function1();
//few lines of code
)
Esempio
Per mostrare la ricorsione indiretta, prendiamo il seguente programma usato per scoprire se un dato numero è pari o dispari dal dato input.
Codice:
import java.util.Scanner;
public class IndirectRecursion (
public static boolean oddNum(int i) (
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0)(
return false;
) else (
return evenNum(i-1);
)
)
public static boolean evenNum(int i) (
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0)(
return true;
) else (
return oddNum(i-1);
)
)
public static void main(String() args) (
Scanner inputNum = new Scanner(System.in);
System.out.print("Give a number: ");
int n = inputNum.nextInt();
if (evenNum(n)) System.out.println(n + " is even");
else System.out.println(n + " is odd");
inputNum.close();
)
)
Produzione:
Esempi di ricorsione in Java
Ecco alcuni altri esempi per risolvere i problemi utilizzando il metodo di ricorsione.
Esempio n. 1 - Sequenza di Fibonacci
Si dice che un insieme di "n" numeri sia in una sequenza di Fibonacci se numero3 = numero1 + numero2, ovvero ogni numero è una somma dei suoi due numeri precedenti. Quindi la sequenza inizia sempre con le prime due cifre come 0 e 1. La terza cifra è una somma di 0 e 1 che risulta in 1, il quarto numero è l'aggiunta di 1 e 1 che risulta in 2 e la sequenza continua.
Controlla il seguente codice in Java per generare una sequenza di Fibonacci:
public class FibonacciSeries(
static int num1=0, num2=1, num3=0;
static void fibonacci(int n)(
if(n>0)(
num3 = num1 + num2;
num1 = num2;
num2 = num3;
System.out.print(" "+num3);
fibonacci(n-1);
)
)
public static void main(String args())(
int n=10;
System.out.print(num1+" "+num2);//printing constant first two digits 0 and 1
fibonacci(n-2);//Since first two numbers are already done
)
)
Produzione:

Qui i primi due numeri vengono inizializzati su 0 e 1 e stampati. Le variabili "num1", "num2" e "num3" vengono utilizzate per generare la sequenza richiesta. La variabile "num3" si ottiene aggiungendo "num1" e "num2" e i numeri vengono spostati di una posizione a sinistra mescolando come mostrato nel codice. La funzione "Fibonacci" viene chiamata in modo ricorsivo qui e ad ogni iterazione, il valore di "n" viene diminuito di 1. Quindi la ricorsione esce non appena "n" raggiunge il valore 0.
Esempio n. 2 - Torre di Hanoi
Questo è un classico problema matematico che sta avendo 3 poli e "n" numero di dischi con dimensioni diverse. Il puzzle è il seguente:
All'inizio, il primo polo avrà i dischi disposti in modo tale che il disco più grande di tutti si trovi in fondo e il più piccolo in cima al palo. L'obiettivo è spostare questi dischi dal primo polo al terzo polo mantenendo i dischi nella stessa posizione di quello del primo. Di seguito sono riportate alcune condizioni da tenere a mente durante lo spostamento di questi dischi:
1. Alla volta è necessario spostare solo un disco.
2. Nel processo, non è consentito posizionare un disco più grande su uno più piccolo.
3. Il secondo polo (medio) può essere usato per mediare durante il trasferimento dei dischi dal primo al secondo polo.
Di seguito è riportato il codice Java che può essere utilizzato per risolvere il puzzle:
Codice:
public class TowerOfHanoi (
public static void main(String() args) (
int count = 3;
tower(count, 'A', 'B', 'C');
)
public static void tower(int first, char disk1, char temp, char disk2) (
if (first == 1) (
System.out.println("Disk 1 from " + disk1 + " to " + disk2);
) else (
tower(first - 1, disk1, disk2, temp);
System.out.println("Disk " + first + " from " + disk1 + " to " + disk2);
tower(first - 1, temp, disk1, disk2);
)
)
)
Produzione:
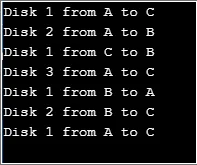
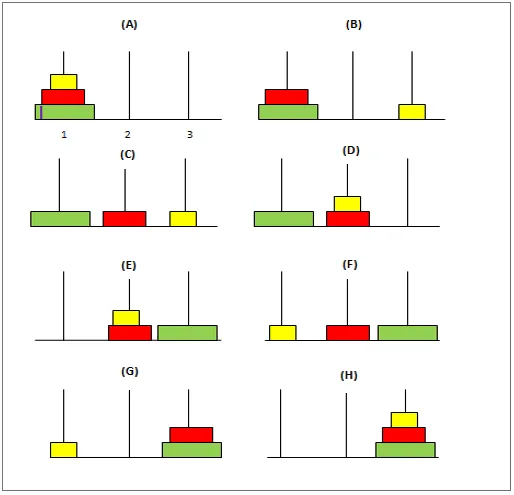
Qui la variabile "count" rappresenta il numero di dischi da utilizzare. La funzione “torre” è la funzione ricorsiva utilizzata per spostare i dischi dall'asta 1 all'asta 3. Una soluzione semplice a questo problema può essere fornita considerando inizialmente 2 dischi.
- Innanzitutto, iniziamo spostando disc1 dall'asta 1 all'asta 2.
- Quindi, spostiamo disc2 sull'asta 3.
- Infine, terminiamo spostando il disco1 sull'asta 3 completando la soluzione richiesta.
Questo stesso principio viene applicato per il numero "n" di dischi spostando (n-1) il disco dall'asta da 1 a 2 e seguendo passaggi simili a quelli sopra indicati.
Vantaggi della ricorsione in Java
- Il codice è facile da scrivere e gestire.
- Il metodo migliore per trovare i risultati in cui è richiesto un numero elevato di iterazioni.
Svantaggi della ricorsione in Java
- Le funzioni ricorsive utilizzano più memoria. Questo perché ogni volta che viene chiamata una funzione ricorsiva; l'allocazione di memoria viene eseguita di nuovo per le variabili nello stack. E la rispettiva allocazione di memoria viene liberata non appena vengono restituiti i valori delle variabili.
- Questo processo di allocazione della memoria richiede più tempo, quindi l'esecuzione è generalmente lenta.
Conclusione
Le funzioni ricorsive sono relativamente più semplici da codificare, ma non sono altrettanto efficienti rispetto agli altri metodi esistenti. Quindi sono principalmente utilizzati nei casi in cui il tempo dedicato allo sviluppo è inferiore e anche dove si può osservare un modello significativo nel problema.
Articoli consigliati
Questa è una guida alla ricorsione in Java. Qui discutiamo i tipi di ricorsione in Java insieme ai suoi diversi esempi con i vantaggi e gli svantaggi. Puoi anche consultare i seguenti articoli per saperne di più-
- JScrollPane in Java
- Funzioni matematiche in Java
- Funzioni matematiche in Java
- Costruttore in Java
- Funzione ricorsiva in Python
- Programma fattoriale in JavaScript