
Formula del margine di errore (sommario)
- Formula del margine di errore
- Esempi di formula Margine di errore (con modello Excel)
- Margine di errore Formula Calculator
Formula del margine di errore
In statistica, calcoliamo l'intervallo di confidenza per vedere dove cadrà il valore dei dati della statistica campione. L'intervallo di valori che sono al di sotto e al di sopra della statistica di esempio in un intervallo di confidenza è noto come Margine di errore. In altre parole, è fondamentalmente il grado di errore nella statistica di esempio. Maggiore è il margine di errore, minore sarà la fiducia nei risultati perché il grado di deviazione in questi risultati è molto elevato. Come suggerisce il nome, il margine di errore è un intervallo di valori sopra e sotto i risultati effettivi. Ad esempio, se otteniamo una risposta in un sondaggio in cui il 70% delle persone ha risposto "bene" e il margine di errore è del 5%, ciò significa che in generale, dal 65% al 75% della popolazione pensa che la risposta sia "buona" .
La formula per Margin of Error -
Margin of Error = Z * S / √n
Dove:
- Punteggio Z - Z.
- S - Deviazione standard di una popolazione
- n - Dimensione del campione
Un'altra formula per calcolare il margine di errore è:
Margin of Error = Z * √((p * (1 – p)) / n)
Dove:
- p - Proporzione del campione (frazione del campione che è un successo)
Ora per trovare il punteggio z desiderato, è necessario conoscere l'intervallo di confidenza del campione perché il punteggio Z dipende da quello. La tabella seguente mostra la relazione tra un intervallo di confidenza e un punteggio z:
| Intervallo di confidenza | Z - Punteggio |
| 80% | 1.28 |
| 85% | 1.44 |
| 90% | 1.65 |
| 95% | 1.96 |
| 99% | 2.58 |
Una volta che conosci l'intervallo di confidenza, puoi usare il valore z corrispondente e calcolare il margine di errore da lì.
Esempi di formula Margine di errore (con modello Excel)
Facciamo un esempio per comprendere meglio il calcolo del margine di errore.
Puoi scaricare questo modello Margine di errore qui - Modello Margine di erroreFormula del margine di errore - Esempio n. 1
Diciamo che stiamo conducendo un sondaggio per vedere qual è il punteggio ottenuto dagli studenti universitari. Abbiamo selezionato 500 studenti a caso e abbiamo chiesto il loro punteggio. La media è 2, 4 su 4 e la deviazione standard è del 30%. Supponiamo che l'intervallo di confidenza sia del 99%. Calcola il margine di errore.
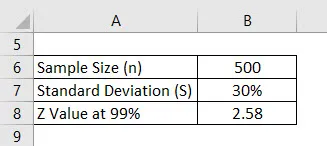
Soluzione:
Il margine di errore viene calcolato utilizzando la formula indicata di seguito
Margine di errore = Z * S / √n
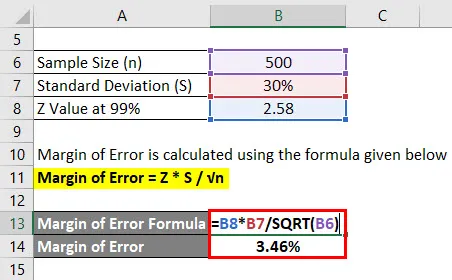
- Margine di errore = 2, 58 * 30% / √ (500)
- Margine di errore = 3, 46%
Ciò significa che, con un livello di confidenza del 99%, il voto medio degli studenti è 2, 4 più o meno 3, 46%.
Formula del margine di errore - Esempio n. 2
Supponiamo che tu stia lanciando sul mercato un nuovo prodotto per la salute, ma sei confuso sul sapore che piacerà alla gente. Sei confuso tra aroma di banana e aroma di vaniglia e hai deciso di condurre un sondaggio. La tua popolazione per questo è di 500.000 che è il tuo mercato di riferimento e da ciò hai deciso di chiedere il parere di 1000 persone e che sarà il campione. Supponiamo che un intervallo di confidenza sia del 90%. Calcola il margine di errore.
Soluzione:
Una volta terminato il sondaggio, hai scoperto che a 470 persone piaceva il sapore di banana e 530 ha chiesto il sapore di vaniglia.
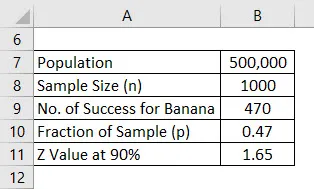
Il margine di errore viene calcolato utilizzando la formula indicata di seguito
Margine di errore = Z * √ ((p * (1 - p)) / n)
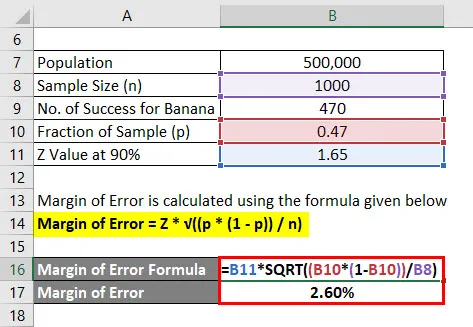
- Margine di errore = 1, 65 * √ ((0, 47 * (1 - 0, 47)) / 1000)
- Margine di errore = 2, 60%
Quindi possiamo affermare che con una sicurezza del 90% che al 47% di tutte le persone piaceva il sapore di banana più o meno il 2, 60%.
Spiegazione
Come discusso in precedenza, il margine di errore ci aiuta a capire se la dimensione del campione del sondaggio è appropriata o meno. Nel caso in cui l'errore di margine sia troppo grande, può succedere che la dimensione del nostro campione sia troppo piccola e che dobbiamo aumentarla in modo che i risultati del campione corrispondano più strettamente ai risultati della popolazione.
Ci sono alcuni scenari in cui il margine di errore non sarà di grande utilità e non ci aiuterà a tenere traccia dell'errore:
- Se le domande del sondaggio non sono progettate e non aiutano a ottenere la risposta richiesta
- Se le persone che stanno rispondendo al sondaggio hanno dei pregiudizi riguardo al prodotto per il quale viene svolto il sondaggio, anche il risultato non sarà molto preciso
- Se il campione scelto stesso è il rappresentante appropriato della popolazione, anche in quel caso i risultati saranno lontani.
Inoltre, un grande presupposto qui è che la popolazione è normalmente distribuita. Quindi se la dimensione del campione è troppo piccola e la distribuzione della popolazione non è normale, il punteggio z non può essere calcolato e non saremo in grado di trovare il margine di errore.
Rilevanza e usi del margine di errore Formula
Ogni volta che utilizziamo i dati di esempio per trovare una risposta pertinente per l'insieme della popolazione, vi sono alcune incertezze e possibilità che il risultato possa discostarsi dal risultato effettivo. Il margine di errore ci dirà che qual è il livello di deviazione è l'output del campione. Dobbiamo ridurre al minimo il margine di errore in modo che i risultati del nostro campione rappresentino la storia reale dei dati sulla popolazione. Quindi abbassare il margine di errore, migliori saranno i risultati. Il margine di errore completa e completa le informazioni statistiche che abbiamo. Ad esempio, se un sondaggio rileva che il 48% delle persone preferisce trascorrere del tempo a casa durante il fine settimana, non possiamo essere così precisi e ci sono alcuni elementi mancanti in tali informazioni. Quando abbiamo introdotto un margine di errore qui, diciamo, il 5%, il risultato sarà interpretato come il 43-53% alla gente piaceva l'idea di essere a casa durante il fine settimana, il che ha perfettamente senso.
Margine di errore Formula Calculator
È possibile utilizzare il seguente calcolatore del margine di errore
| Z | |
| S | |
| √ n | |
| Margine di errore | |
| Margine di errore | = |
|
|
Articoli consigliati
Questa è stata una guida alla formula Margin of Error. Qui discutiamo come calcolare il margine di errore insieme ad esempi pratici. Forniamo anche un calcolatore del margine di errore con modello Excel scaricabile. Puoi anche consultare i seguenti articoli per saperne di più -
- Guida alla formula di ammortamento a quote costanti
- Esempi di formula del tempo di raddoppio
- Come calcolare l'ammortamento?
- Formula per il teorema del limite centrale
- Punteggio Altman Z | Definizione | Esempi
- Formula di ammortamento | Esempi con modello di Excel