Unisci ordina in JavaScript - Diversi tipi di proprietà

Introduzione a Merge Sort in JavaScript

Gli algoritmi di ordinamento sono molto importanti in Informatica. L'output dell'ordinamento consiste nel disporre gli elementi di un elenco in base a un determinato ordine (crescente o decrescente). Unisci ordinamento in JavaScript è uno degli algoritmi di ordinamento più efficienti disponibili in quanto si basa sul concetto di divisione e conquista. Come suggerisce il nome, prima dividi il problema più grande in piccoli problemi piuttosto che risolvere i problemi più piccoli al fine di risolvere il problema più grande. Concettualmente, Merge sort è una combinazione di due algoritmi di base chiamati MERGE e MERGE_SORT.

che funziona come segue:

1. Dividi l'elenco non ordinato in n numero di elenchi secondari a elemento singolo (n è il numero totale di elementi nell'elenco non ordinato).
2. Unisci ripetutamente gli elenchi secondari in elenchi ordinati finché non esiste un solo elenco ordinato.

Implementazione di Merge Sort in JavaScript

L'algoritmo MERGE segue la procedura di combinazione di due elenchi ordinati in un elenco ordinato.

Esempio: supponiamo che ci siano due elenchi, ovvero Elenco 1 (1, 5, 3) e Elenco 2 (7, 2, 9).

1. Prima ordina entrambi gli elenchi.

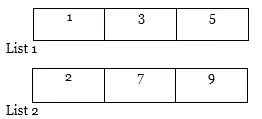
Ora vedremo e applicheremo la tecnica E su di essa.

2. Quindi, creeremo un nuovo elenco di dimensioni x + y in cui x è il numero di elementi nell'elenco 1 e y è il numero di elementi nell'elenco 2.

Nel nostro caso x = 3 e y = 3, quindi x + y = 6.

3. Ora, abbiamo due puntatori.
Un primo puntatore che punta sulla prima posizione dell'elenco 1 e Secondo puntatore che punta sulla prima posizione dell'elenco 2.

4. Quindi confronteremo il valore di entrambi i puntatori. Il puntatore con un valore inferiore, copia quell'elemento in Elenco 3 e sposta il puntatore a destra dell'elenco con un valore più piccolo e l'elenco risultante (cioè Elenco 1 ed Elenco 3)

5. Allo stesso modo, eseguire nuovamente il passaggio 4.

Ulteriore attraversamento …

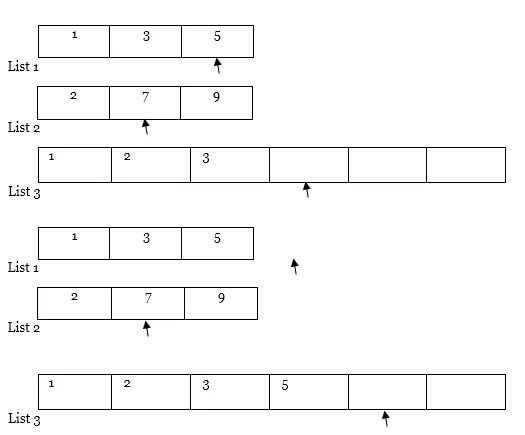
Nota : se uno degli elenchi (ovvero l'elenco 1 o l'elenco 2) viene completamente attraversato come nel caso, quindi copiare l'intero contenuto di un altro elenco dal puntatore all'elenco dei risultati (ovvero l'elenco 3) come segue.

pseudocodice

Function merge (sublist1, sublist2) (
Create var for result list
While sublist1 length > 0 and sublist2 length > 0
If sublist1(0) < sublist2(0) Copy the sublist1 pointer value to result list and Shift pointer of sublist1 to right
else
Copy the sublist2 pointer value to result list and Shift pointer of sublist2 to right
Return concat sublist1 or sublist2 (depending if node1 is empty or not)

L'algoritmo MERGE_SORT divide l'elenco specificato non ordinato in base alla dimensione minima, quindi chiama l'algoritmo MERGE per combinare l'elenco nel nuovo elenco ordinato.

pseudocodice

function mergeSort(list) (
If list length < 2
Return list
Create var for middle index of list
Create var for left index of list
Create var for right index of list
Recursively call mergeSort function
)

Esempio

Qui stiamo seguendo l'implementazione di Merge Sort top-down. Inizia dall'alto e procede verso il basso, con ogni turno ricorsivo che pone la stessa domanda "Cosa è necessario fare per ordinare l'elenco?" E avere la risposta è "Dividi l'elenco in due, effettua una chiamata ricorsiva e unisci il risultati”.

Codice in Javascript

// Split the list into halves and merge them recursively
function mergeSort (list) (
if (list.length < 2) (
return list;// return once we hit a list with a single element
)
var mid = Math.floor(list.length / 2);
var left = mergeSort(list.slice(0, mid));
var right = mergeSort(list.slice(mid));
return merge(left, right);
)
// compare the lists element by element and return the concatenated resultList
function merge (sublist1, sublist2) (
var resultList = ();
while (sublist1.length > 0 && sublist2.length > 0)
resultList.push(sublist1(0) < sublist2(0)? sublist1.shift() : sublist2.shift());
return resultList.concat(sublist1.length? sublist1 : sublist2);
)
const list = (6, 5, 3, 1, 8, 7, 2, 4, 2, 5, 1, 2, 3) console.log(mergeSort(list)) //( 1, 1, 2, 2, 2, 3, 3, 4, 5, 5, 6, 7, 8 )

La funzione principale dell'ordinamento di tipo merge dividerà l'elenco specificato in elenchi più piccoli in ogni iterazione della chiamata ricorsiva. Non dimenticare che la ricorsione richiede la condizione di base per evitare la ricorsione infinita. Nel nostro caso, abbiamo:

if (list.length < 2) (
return list;// return once we hit a list with a single element
)

Dopo aver impostato la condizione di base per la ricorsione, identificheremo l'indice centrale per dividere l'elenco dato nell'elenco secondario sinistro e destro, come puoi vedere sopra nel diagramma di esempio. Quindi dobbiamo unire la sotto-lista di sinistra e la sotto-lista di destra che vedremo ora, nella funzione di unione sopra, dobbiamo assicurarci che stiamo ordinando tutti gli elementi nella sotto-lista di sinistra e sotto-destra elenco. Il modo in cui lo faremo è usando un ciclo while. All'interno del ciclo while, confronteremo l'elemento nella sotto-lista di sinistra e l'elemento nella sotto-lista di destra uno per uno. Possiamo inserire il più piccolo dei due nell'elenco dei risultati e spostare di conseguenza il cursore dell'elenco secondario sinistro e dell'elenco secondario destro. Infine, dobbiamo concatenare l'elenco dei risultati. Questo è molto importante! Se non facciamo questo ultimo passaggio qui, avremo un elenco incompleto di elementi alla fine perché la condizione del ciclo while fallirà quando uno dei due puntatori raggiunge la fine.

Produzione:

Proprietà di Unisci ordinamento

1. Unisci ordinamento è stabile in quanto lo stesso elemento in un array mantiene le posizioni originali l'uno rispetto all'altro.
2. Unisci ordinamento non è "in atto" poiché durante l'unione crea una copia dell'intero elenco. A causa di ciò, la complessità dello spazio (O (n)) di questo algoritmo è in realtà maggiore di altri e non deve essere utilizzata in problemi complessi in cui lo spazio è premium.
3. La complessità temporale complessiva dell'ordinamento Merge è O (nLogn). È più efficiente come anche nel caso peggiore, il runtime è O (nlogn).

Conclusione

Unisci le complessità migliori, peggiori e nel caso medio sono le stesse che lo rendono un algoritmo più efficiente. Funziona più velocemente di altre tecniche di ordinamento. Unisci ordinamento può essere applicato a file di qualsiasi dimensione. È altamente parallelizzabile grazie all'uso del metodo divide-and-conquer. Al fine di sviluppare solide basi di informatica, si consiglia di comprendere a fondo i diversi algoritmi di ordinamento.

Articolo raccomandato

Questa è stata una guida per unire l'ordinamento in JavaScript. Qui discutiamo Introduzione a Merge Sort in JavaScript e l'implementazione insieme a Proprietà. Puoi anche consultare i nostri altri articoli suggeriti per saperne di più -

1. Funzioni matematiche JavaScript
2. Introduzione a JavaScript
3. I migliori frame Javascript
4. Strumenti JavaScript
5. I 6 migliori algoritmi di ordinamento in JavaScript