
Introduzione alla distribuzione binomiale in R
Questo articolo descrive come utilizzare le distribuzioni binomiali in R per le poche operazioni coinvolte nelle distribuzioni di probabilità. Business Analysis utilizza la probabilità binomiale per un problema complesso. R ha numerose funzioni integrate per il calcolo delle distribuzioni binomiali utilizzate nelle interferenze statistiche. La distribuzione binomiale nota anche come prove di Bernoulli prende due tipi di successo p e fallimento S. L'obiettivo principale del modello di distribuzione binomiale è quello di calcolare i possibili risultati di probabilità monitorando un numero specifico di possibilità positive ripetendo il processo un determinato numero di volte . Dovrebbero avere due possibili risultati (successo / fallimento), quindi il risultato è dicotomico. La notazione matematica predefinita è p = successo, q = 1-p.
Esistono quattro funzioni associate alle distribuzioni binomiali. Sono dbinom, pbinom, qbinom, rbinom. La sintassi formattata è riportata di seguito:
Sintassi
- dbinom (x, dimensione, prob)
- pbinom (x, dimensione, prob)
- qbinom (x, size, prob) o qbinom (x, size, prob, lower_tail, log_p)
- rbinom (x, dimensione, prob)
La funzione ha tre argomenti: il valore x è un vettore di quantili (da 0 a n), la dimensione è il numero di tentativi di scia, prob indica probabilità per ogni tentativo. Vediamo uno per uno con un esempio.
1) dbinom ()
È una funzione di densità o distribuzione. I valori vettoriali devono essere un numero intero non deve essere un numero negativo. Questa funzione tenta di trovare un certo successo in un no. di prove fisse.
Una distribuzione binomiale accetta dimensioni e valori x. ad esempio, size = 6, i possibili valori x sono 0, 1, 2, 3, 4, 5, 6 che implica P (X = x).
n <- 6; p<- 0.6; x <- 0:n
dbinom(x, n, p)
Produzione:
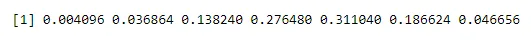
Fare probabilità a uno
n <- 6; p<- 0.6; x <- 0:n
sum(dbinom(x, n, p))
Produzione:
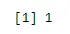
Esempio 1 - Il database ospedaliero mostra che i pazienti affetti da cancro ne muoiono per il 65%. Quale sarà la probabilità che su 5 pazienti scelti a caso tra i quali 3 guariranno?
Qui applichiamo la funzione dbinom. La probabilità che 3 recuperi utilizzando la distribuzione della densità in tutti i punti.
n = 5, p = 0, 65, x = 3
dbinom(3, size=5, prob=0.65)
Produzione:

Per il valore x da 0 a 3:
dbinom(0, size=5, prob=0.65) +
+ dbinom(1, size=5, prob=0.65) +
+ dbinom(2, size=5, prob=0.65) +
+ dbinom(3, size=5, prob=0.65)
Produzione:
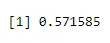
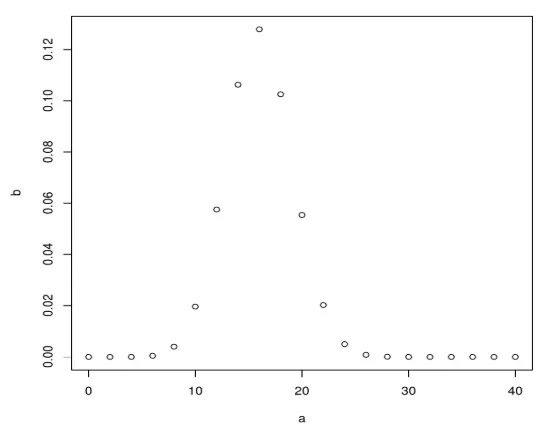
Quindi, crea un campione di 40 carte e incrementale di 2 creando anche un binomio usando dbinom.
a <- seq(0, 40, by = 2)
b <- dbinom(a, 40, 0.4)
plot(a, b)
Produce il seguente output dopo aver eseguito il codice sopra, La distribuzione binomiale viene tracciata usando la funzione plot ().
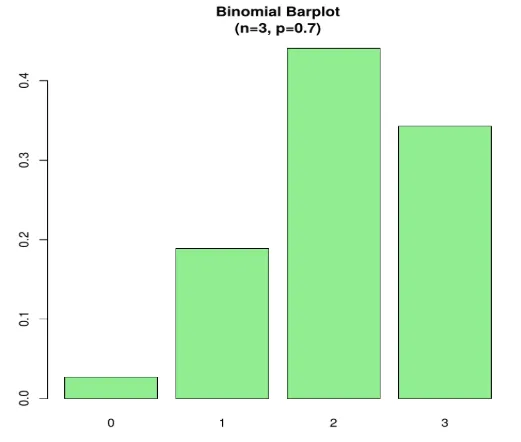
Esempio 2 - Consideriamo uno scenario, supponiamo che una probabilità che uno studente presti un libro da una biblioteca sia di 0, 7. Ci sono 6 studenti in biblioteca, qual è la probabilità che 3 di loro prestino un libro?
qui P (X = 3)
Codice:
n=3; p=.7; x=0:n; prob=dbinom(x, n, p);
barplot(prob, names.arg = x, main="Binomial Barplot\n(n=3, p=0.7)", col="lightgreen")
Il grafico seguente mostra quando p> 0, 5, quindi la distribuzione binomiale è distorta positivamente come visualizzato.
Produzione:
2) Pbinom ()
calcola le probabilità cumulative di binomiale o CDF (P (X <= x)).
Esempio 1:
x <- c(0, 2, 5, 7, 8, 12, 13)
pbinom(x, size=20, prob=.2)
Produzione:

Esempio 2: Dravid segna un wicket sul 20% dei suoi tentativi quando lancia. Se ci lancia 5 volte, quale sarebbe la probabilità di segnare 4 o meno wicket?
La probabilità di successo è 0, 2 qui e durante 5 tentativi otteniamo
pbinom(4, size=5, prob=.2)
Produzione:
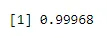
Esempio 3: il 4% degli americani è nero. Trova la probabilità di 2 studenti neri selezionando casualmente 6 studenti da una classe di 100 senza sostituzione.
Quando R: x = 4 R: n = 6 R: p = 0. 0 4
pbinom(4, 6, 0.04)
Produzione:-
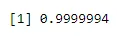
3) qbinom ()
È una funzione quantile e fa l'inverso della funzione di probabilità cumulativa. Il valore cumulativo corrisponde a un valore di probabilità.
Esempio: quante code avranno una probabilità di 0, 2 quando una moneta viene lanciata 61 volte.
a <- qbinom(0.2, 61, 1/2)
print(a)
Produzione:-
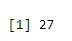
4) rbinom ()
Genera numeri casuali. Risultati diversi producono output casuali diversi, utilizzati nel processo di simulazione.
Esempio:-
rbinom(30, 5, 0.5)
rbinom(30, 5, 0.5)
Produzione:-

Ogni volta che lo eseguiamo, si ottengono risultati casuali.
rbinom(200, 4, 0.4)
Produzione:-

Qui lo facciamo assumendo il risultato di 30 lanci di monete in un solo tentativo.
rbinom(30, 1, 0.5)
Produzione:-
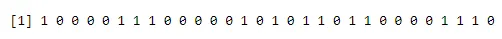
Utilizzando barplot:
a<-rbinom(30, 1, 0.5)
print(a)
barplot(table(a),>
Produzione:-
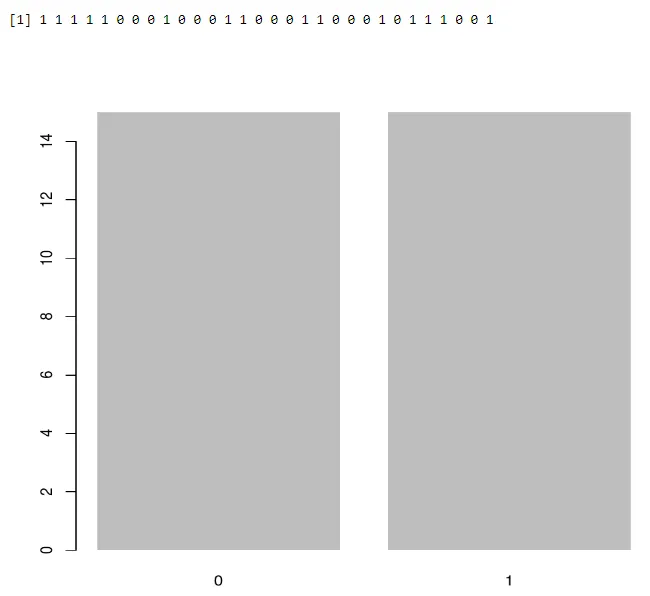
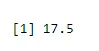
Per trovare la media del successo
output <-rbinom(10, size=60, 0.3)
mean(output)
Produzione:-
Conclusione - Distribuzione binomiale in R
Quindi, in questo documento abbiamo discusso della distribuzione binomiale in R. Abbiamo simulato usando vari esempi in frammenti di R studio e R e abbiamo anche descritto le funzioni integrate che aiutano a generare calcoli binomiali. Il calcolo della distribuzione binomiale in R utilizza calcoli statistici. Pertanto, una distribuzione binomiale aiuta a trovare probabilità e ricerca casuale usando una variabile binomiale.
Articoli consigliati
Questa è una guida alla distribuzione binomiale in R. Qui discuteremo un'introduzione e le sue funzioni associate alla distribuzione binomiale insieme alla sintassi e agli esempi appropriati. Puoi anche consultare i nostri altri articoli suggeriti per saperne di più -
- Formula di distribuzione binomiale
- Economia vs impresa
- Tecniche di analisi aziendale
- Distribuzioni Linux