Differenza tra regressione lineare e regressione logistica
Il seguente articolo Regressione lineare e regressione logistica fornisce le differenze più importanti tra i due, ma prima vedremo cosa significa Regressione?
Regressione
La regressione è fondamentalmente una misura statistica per determinare la forza della relazione tra una variabile dipendente, ovvero l'uscita Y e una serie di altre variabili indipendenti, ovvero X 1, X 2 e così via. L'analisi di regressione viene utilizzata essenzialmente per la previsione e la previsione.
Che cos'è la regressione lineare?
La regressione lineare è un algoritmo basato sul dominio di apprendimento supervisionato dell'apprendimento automatico. Eredita una relazione lineare tra le sue variabili di input e la singola variabile di output in cui la variabile di output è di natura continua. Viene utilizzato per prevedere il valore dell'output, diciamo Y dagli input, diciamo X. Quando si considera un solo input, si parla di regressione lineare semplice.
Può essere classificato in due categorie principali:
1. Regressione semplice
Principio di funzionamento: l'obiettivo principale è scoprire l'equazione di una linea retta che si adatta meglio ai dati campionati. Questa equazione descrive algebricamente la relazione tra le due variabili. La retta più adatta si chiama linea di regressione.
Y = β 0 + β 1 X
Dove,
β rappresenta le caratteristiche
β 0 rappresenta l'intercetta
β 1 rappresenta il coefficiente della funzione X
2. Regressione multivariabile
Viene utilizzato per prevedere una correlazione tra più di una variabile indipendente e una variabile dipendente. La regressione con più di due variabili indipendenti si basa sull'adattamento della forma alla costellazione di dati su un grafico multidimensionale. La forma della regressione dovrebbe essere tale da ridurre al minimo la distanza della forma da ogni punto dati.
Un modello di relazione lineare può essere rappresentato matematicamente come di seguito:
Y = β 0 + β 1 X 1 + β 2 X 2 + β 3 X 3 + ……. + β n X n
Dove,
β rappresenta le caratteristiche
β 0 rappresenta l'intercetta
β 1 rappresenta il coefficiente della caratteristica X 1
β n rappresenta il coefficiente della caratteristica X n
Vantaggi e svantaggi della regressione lineare
Di seguito sono riportati i vantaggi e gli svantaggi:
vantaggi
- Per la sua semplicità, è ampiamente utilizzato come modello per previsioni e inferenze.
- Si concentra sull'analisi e la preelaborazione dei dati. Quindi, si occupa di dati diversi senza preoccuparsi dei dettagli del modello.
svantaggi
- Funziona in modo efficiente quando i dati sono normalmente distribuiti. Pertanto, per una modellizzazione efficiente, la collinearità deve essere evitata.
Che cos'è la regressione logistica?
È una forma di regressione che consente la previsione di variabili discrete mediante una combinazione di predittori continui e discreti. Ne risulta una trasformazione unica di variabili dipendenti che influisce non solo sul processo di stima ma anche sui coefficienti di variabili indipendenti. Affronta la stessa domanda che fa la regressione multipla ma senza ipotesi distributive sui predittori. Nella regressione logistica la variabile di risultato è binaria. Lo scopo dell'analisi è di valutare gli effetti di più variabili esplicative, che possono essere numeriche o categoriche o entrambe.
Tipi di regressione logistica
Di seguito sono riportati i 2 tipi di regressione logistica:
1. Regressione logistica binaria
È usato quando la variabile dipendente è dicotomica, cioè come un albero con due rami. Viene utilizzato quando la variabile dipendente non è parametrica.
Usato quando
- Se non c'è linearità
- Esistono solo due livelli della variabile dipendente.
- Se la normalità multivariata è dubbia.
2. Regressione logistica multinomiale
L'analisi della regressione logistica multinomiale richiede che le variabili indipendenti siano metriche o dicotomiche. Non fa alcuna ipotesi di linearità, normalità e omogeneità di varianza per le variabili indipendenti.
Viene utilizzato quando la variabile dipendente ha più di due categorie. Viene utilizzato per analizzare le relazioni tra una variabile dipendente non metrica e variabili indipendenti metriche o dicotomiche, quindi confronta più gruppi attraverso una combinazione di regressioni logistiche binarie. Alla fine, fornisce un insieme di coefficienti per ciascuno dei due confronti. I coefficienti per il gruppo di riferimento sono considerati tutti zeri. Infine, la previsione viene effettuata in base alla probabilità risultante più elevata.
Vantaggio della regressione logistica: è una tecnica molto efficiente e ampiamente utilizzata in quanto non richiede molte risorse computazionali e non richiede alcuna ottimizzazione.
Svantaggio della regressione logistica: non può essere utilizzato per risolvere problemi non lineari.
Confronto testa a testa tra regressione lineare e regressione logistica (infografica)
Di seguito sono riportate le 6 principali differenze tra Regressione lineare e Regressione logistica 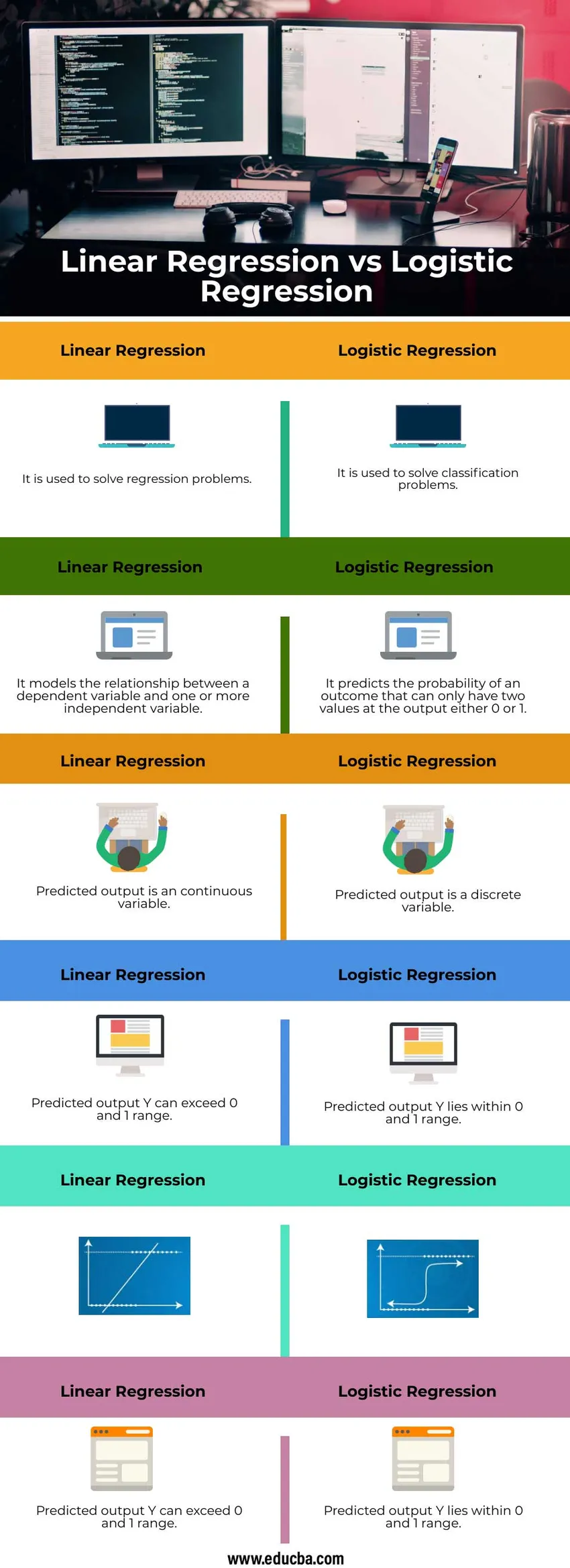
Differenza chiave tra la regressione lineare e la regressione logistica
Discutiamo alcune delle principali differenze chiave tra regressione lineare e regressione logistica
Regressione lineare
- È un approccio lineare
- Usa una linea retta
- Non può accettare variabili categoriali
- Deve ignorare le osservazioni con valori mancanti della variabile numerica indipendente
- L'uscita Y è data come
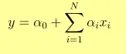
- 1 aumento di unità in x aumenta Y di α
applicazioni
- Prevedere il prezzo di un prodotto
- Prevedere il punteggio in una partita
Regressione logistica
- È un approccio statistico
- Utilizza una funzione sigmoide
- Può prendere variabili categoriali
- Può prendere decisioni anche se sono presenti osservazioni con valori mancanti
- L'output Y è dato come, dove z è dato come
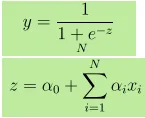
- L'aumento di 1 unità in x aumenta Y di probabilità di log di α
- Se P è la probabilità di un evento, allora (1-P) è la probabilità che non si verifichi. Probabilità di successo = P / 1-P
applicazioni
- Prevedere se oggi pioverà o no.
- Prevedere se un'e-mail è o meno uno spam.
Tabella di confronto tra regressione lineare e regressione logistica
Discutiamo il confronto tra la regressione lineare e la regressione logistica
|
Regressione lineare |
Regressione logistica |
| Viene utilizzato per risolvere i problemi di regressione | Viene utilizzato per risolvere i problemi di classificazione |
| Modella la relazione tra una variabile dipendente e una o più variabili indipendenti | Prevede la probabilità di un risultato che può avere solo due valori in uscita 0 o 1 |
| L'output previsto è una variabile continua | L'output previsto è una variabile discreta |
| L'uscita prevista Y può superare l'intervallo 0 e 1 | L'uscita prevista Y è compresa nell'intervallo 0 e 1 |
 | 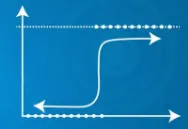 |
| L'uscita prevista Y può superare l'intervallo 0 e 1 | Uscita prevista |
Conclusione
Se le funzionalità non contribuiscono alla previsione o se sono molto correlate tra loro, aggiunge rumore al modello. Pertanto, le funzionalità che non contribuiscono abbastanza al modello devono essere rimosse. Se le variabili indipendenti sono altamente correlate, può causare un problema di multi-collinearità, che può essere risolto eseguendo modelli separati con ciascuna variabile indipendente.
Articoli consigliati
Questa è stata una guida alla regressione lineare e alla regressione logistica. Qui discutiamo le differenze chiave tra Regressione lineare e Regressione logistica con infografica e tabella di confronto. Puoi anche dare un'occhiata ai seguenti articoli per saperne di più–
- Data Science vs Data Visualization
- Apprendimento automatico vs rete neurale
- Apprendimento supervisionato vs apprendimento profondo
- Regressione logistica in R