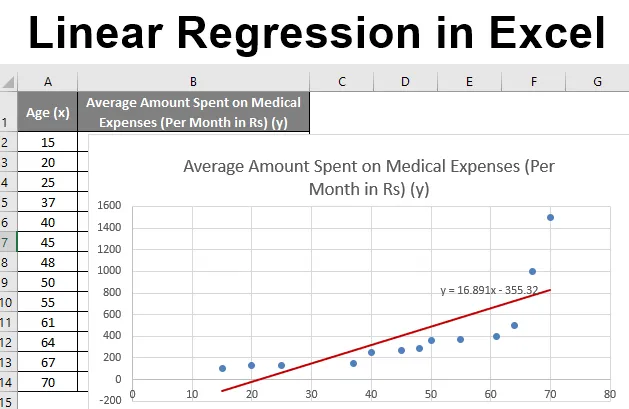
Regressione lineare in Excel - Come eseguire la regressione lineare in Excel?

Regressione lineare in Excel (sommario)

Introduzione alla regressione lineare in Excel
Metodi per l'utilizzo della regressione lineare in Excel

Introduzione alla regressione lineare in Excel

La regressione lineare è una tecnica / metodo statistico utilizzato per studiare la relazione tra due variabili quantitative continue. In questa tecnica, le variabili indipendenti vengono utilizzate per prevedere il valore di una variabile dipendente. Se esiste solo una variabile indipendente, allora è una semplice regressione lineare e se un numero di variabili indipendenti è più di una, allora è una regressione lineare multipla. I modelli di regressione lineare hanno una relazione tra variabili dipendenti e indipendenti adattando un'equazione lineare ai dati osservati. Linear si riferisce al fatto che utilizziamo una linea per adattare i nostri dati. Le variabili dipendenti utilizzate nell'analisi di regressione sono anche chiamate variabili di risposta o previste e le variabili indipendenti sono anche chiamate variabili esplicative o predittori.

Una linea di regressione lineare ha un'equazione del tipo: Y = a + bX;

Dove:

X è la variabile esplicativa,
Y è la variabile dipendente,
b è la pendenza della linea,
a è l'intercetta y (ovvero il valore di y quando x = 0).

Il metodo dei minimi quadrati viene generalmente utilizzato nella regressione lineare che calcola la linea di adattamento migliore per i dati osservati minimizzando la somma dei quadrati di deviazione dei punti di dati dalla linea.

Metodi per l'utilizzo della regressione lineare in Excel

Questo esempio illustra i metodi per eseguire l'analisi della regressione lineare in Excel. Diamo un'occhiata ad alcuni metodi.

Puoi scaricare questo modello Excel di regressione lineare qui - Modello Excel di regressione lineare

Metodo n. 1: grafico a dispersione con una linea di tendenza

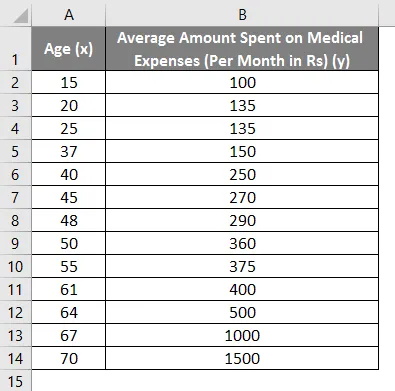
Supponiamo di avere un set di dati di alcuni individui con la loro età, indice di biomassa (BMI) e l'importo da loro speso per le spese mediche in un mese. Ora, con una visione delle caratteristiche degli individui come l'età e l'IMC, desideriamo scoprire come queste variabili influenzano le spese mediche, e quindi usarle per effettuare la regressione e stimare / prevedere le spese mediche medie per alcuni individui specifici. Vediamo innanzitutto come solo l'età influisce sulle spese mediche. Vediamo il set di dati:

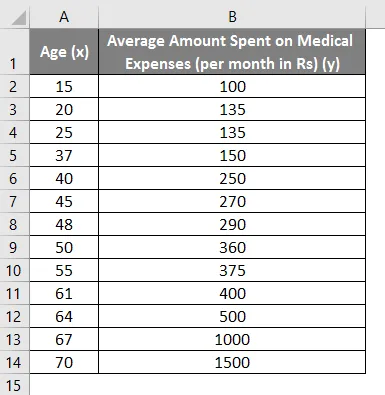
Importo delle spese mediche = b * età + a

Seleziona le due colonne del set di dati (xey), comprese le intestazioni.

Fai clic su "Inserisci" ed espandi il menu a discesa per "Grafico a dispersione" e seleziona la miniatura "Scatter" (prima)

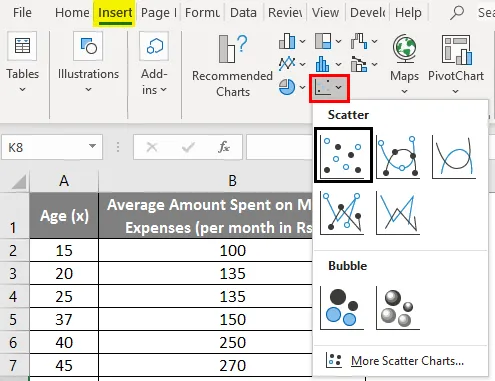
Ora apparirà un diagramma a dispersione e su questo tracciamo la linea di regressione. Per fare ciò, fai clic con il pulsante destro del mouse su qualsiasi punto dati e seleziona "Aggiungi linea di tendenza"

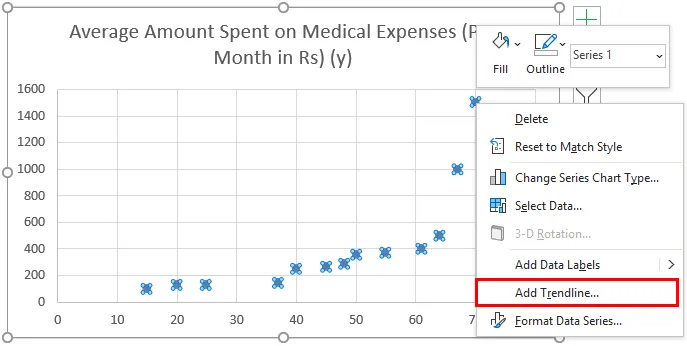
Ora nel riquadro "Formatta linea di tendenza" sulla destra, seleziona "Linea di tendenza lineare" e "Visualizza equazione sul grafico".

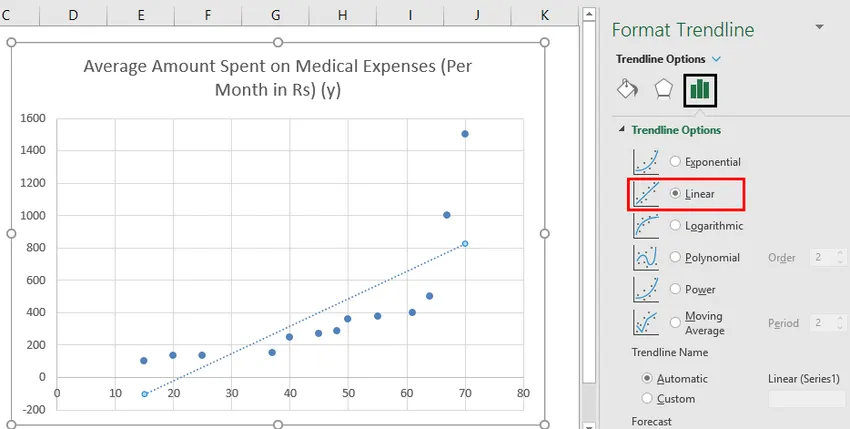
Seleziona "Visualizza equazione sul grafico".

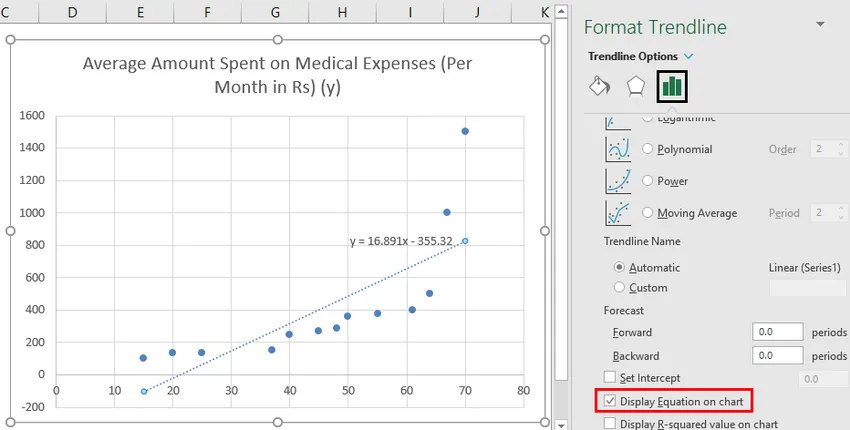
Possiamo improvvisare il grafico secondo i nostri requisiti, come aggiungere titoli degli assi, cambiare la scala, il colore e il tipo di linea.

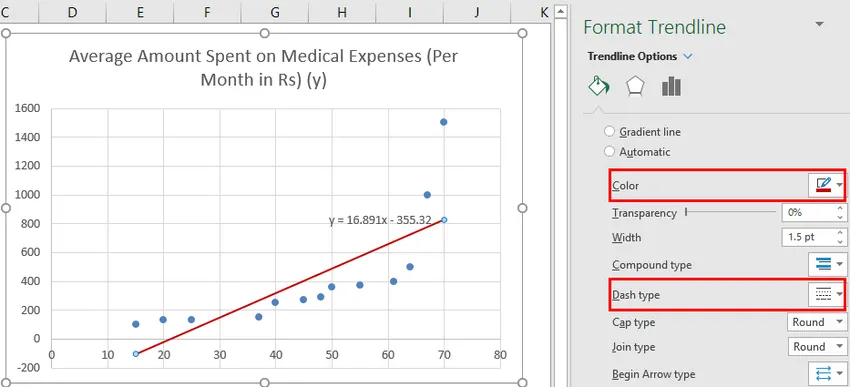
Dopo aver improvvisato il grafico, questo è l'output che otteniamo.

Nota: in questo tipo di grafico di regressione, la variabile dipendente deve essere sempre sull'asse y e indipendente sull'asse x. Se il grafico viene tracciato in ordine inverso, scambiare gli assi in un grafico o scambiare le colonne nel set di dati.

Metodo n. 2 - Metodo aggiuntivo Analysis ToolPak

Analysis ToolPak a volte non è abilitato per impostazione predefinita e dobbiamo farlo manualmente. Fare così:

Fai clic sul menu "File".

Successivamente fai clic su "Opzioni".

Seleziona "Componenti aggiuntivi di Excel" nella casella "Gestisci" e fai clic su "Vai"

Seleziona 'Analysis ToolPak' -> 'OK'

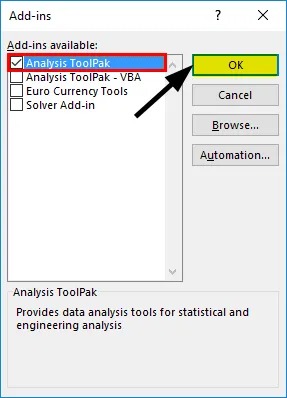
Ciò aggiungerà gli strumenti "Analisi dei dati" alla scheda "Dati". Ora eseguiamo l'analisi di regressione:

Fai clic su "Analisi dei dati" nella scheda "Dati"

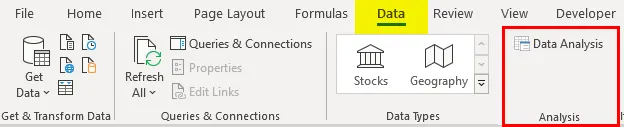
Seleziona 'Regressione' -> 'OK'

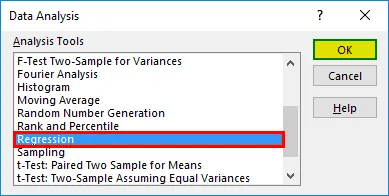
Apparirà una finestra di dialogo di regressione. Selezionare l'intervallo di input Y e l'intervallo di input X (spese mediche ed età, rispettivamente). In caso di regressione lineare multipla, possiamo selezionare più colonne di variabili indipendenti (come se desideriamo vedere l'impatto dell'IMC anche sulle spese mediche).
Seleziona la casella "Etichette" per includere le intestazioni.
Scegli l'opzione 'output' desiderata.
Seleziona la casella di controllo "Residui" e fai clic su "OK".

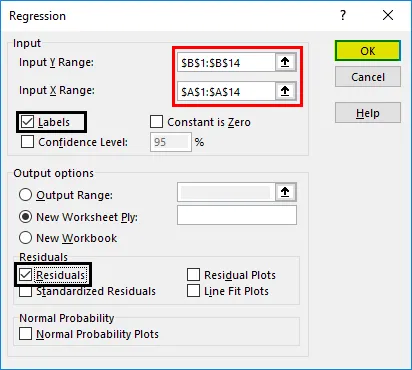
Ora il nostro output dell'analisi di regressione verrà creato in un nuovo foglio di lavoro, indicando le statistiche di regressione, ANOVA, i residui e i coefficienti.

Interpretazione dell'output:

Regressione Statistics indica in che misura l'equazione di regressione si adatta ai dati:

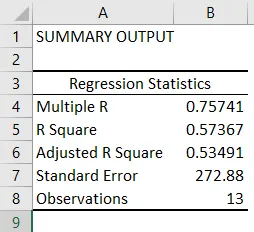
Multiple R è il coefficiente di correlazione che misura la forza della relazione lineare tra due variabili. Si trova tra -1 e 1 e il suo valore assoluto rappresenta la forza della relazione con un valore elevato che indica una relazione più forte, un valore basso che indica un valore negativo e uno zero che non indica alcuna relazione.
R Square è il coefficiente di determinazione utilizzato come indicatore di bontà di adattamento. Si trova tra 0 e 1, con un valore vicino a 1 che indica che il modello è adatto. In questo caso, 0, 57 = 57% dei valori y sono spiegati dai valori x.
Il quadrato R rettificato è il quadrato R rettificato per il numero di predittori in caso di regressione lineare multipla.
L'errore standard descrive la precisione dell'analisi di regressione.
Osservazioni mostra il numero di osservazioni modello.
Anova racconta il livello di variabilità all'interno del modello di regressione.

Questo non è generalmente usato per una semplice regressione lineare. Tuttavia, i "valori di significatività F" indicano quanto siano affidabili i nostri risultati, con un valore maggiore di 0, 05 che suggerisce di scegliere un altro predittore.

I coefficienti è la parte più importante utilizzata per costruire l'equazione di regressione.

Quindi, la nostra equazione di regressione sarebbe: y = 16.891 x - 355.32. Questo è lo stesso del metodo 1 (grafico a dispersione con una linea di tendenza).

Ora, se vogliamo prevedere le spese mediche medie quando l'età è di 72 anni:

Quindi y = 16.891 * 72 -355.32 = 860.832

Quindi in questo modo possiamo prevedere i valori di y per qualsiasi altro valore di x.

I residui indicano la differenza tra valori effettivi e previsti.

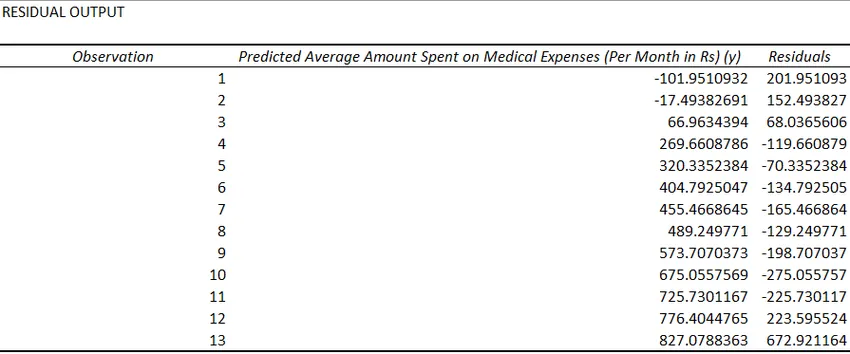
L'ultimo metodo per la regressione non è così comunemente usato e richiede funzioni statistiche come pendenza (), intercept (), correl (), ecc. Per eseguire l'analisi di regressione.

Cose da ricordare sulla regressione lineare in Excel

L'analisi di regressione viene generalmente utilizzata per vedere se esiste una relazione statisticamente significativa tra due insiemi di variabili.
Viene utilizzato per prevedere il valore della variabile dipendente in base ai valori di una o più variabili indipendenti.
Ogni volta che desideriamo adattare un modello di regressione lineare a un gruppo di dati, l'intervallo di dati deve essere attentamente osservato come se usassimo un'equazione di regressione per prevedere qualsiasi valore al di fuori di questo intervallo (estrapolazione), quindi potrebbe portare a risultati errati.

Articoli consigliati

Questa è una guida alla regressione lineare in Excel. Qui discutiamo su come eseguire la regressione lineare in Excel insieme a esempi pratici e template Excel scaricabili. Puoi anche consultare i nostri altri articoli suggeriti: