Ordinamento degli algoritmi in Java - Diversi tipi di algoritmi di ordinamento in Java

• Introduzione agli algoritmi di ordinamento in Java

Introduzione agli algoritmi di ordinamento in Java

Ordinare le informazioni in un certo ordine, spesso all'interno di un framework simile ad un array, significa organizzarle. È possibile utilizzare requisiti di sequenza diversi, quelli più diffusi sono l'ordinamento di numeri dal minimo al maggiore o viceversa o l'ordinamento lessicografico di stringhe. Tratteremo algoritmi diversi, da alternative inefficaci ma intuitive a algoritmi efficienti implementati in modo efficace in Java e in altre lingue se siete interessati a come deve funzionare l'ordinamento.

Diversi algoritmi di ordinamento in Java

Esistono diversi algoritmi di ordinamento e non tutti sono ugualmente efficaci. Per confrontarli e vedere quali funzionano meglio, analizzeremo le loro complessità temporali.

1. Ordinamento inserzione
2. Bubble Sort
3. Ordinamento selezione
4. Unisci ordinamento
5. heapsort

1. Ordinamento inserzione

Il concetto alla base di Insertion Sort divide l'intervallo in sottoarray che sono ordinati e non ordinati. La parte classificata è all'inizio della durata 1 e corrisponde al primo componente (lato sinistro) dell'array. Passiamo attraverso l'array ed espandiamo la parte classificata dell'array di un componente durante ogni iterazione. Quando espandiamo, posizioniamo l'elemento nuovo nell'array secondario ordinato. Lo facciamo spostando tutti gli elementi a destra fino a quando non troviamo che non dobbiamo cambiare il primo componente. Quando la parte in grassetto viene ordinata in ordine crescente, ad esempio, nel seguente array, si verifica:

1. 3 5 7 8 4 2 1 9 6: considera 4 e inserendo questo è ciò di cui abbiamo bisogno. Stiamo cambiando da 8> 4
2. 2. 3 5 7 x 8 2 1 9 6
3. 3 5 x 7 8 2 1 9 6
4. 3 x 5 7 8 2 1 9 6
5. 3 4 5 7 8 2 1 9 6

Codice:

public class InsertionSortEx (
public static void insertionSort(int() arr) (
for (int x = 1; x < arr.length; x++) (
int current = arr(x);
int y = x - 1;
while(y >= 0 && current < arr(y)) (
arr(y+1) = arr(y);
y--;
)
arr(y+1) = current;
)
)
public static void main(String a())(
int() arr1 = (3, 5, 7, 8, 4, 2, 1, 9, 6);
System.out.println("Before Sorting");
for(int x:arr1)(
System.out.print(x+" ");
)
System.out.println();
insertionSort(arr1);//sorting array using insertion sort
System.out.println("After Insertion Sorting");
for(int x:arr1)(
System.out.print(x+" ");
)
)
)

Produzione:

Seguendo questo metodo, un componente ha esteso la parte ordinata, ora abbiamo cinque anziché quattro elementi. Ogni iterazione fa questo e l'intero array verrà ordinato alla fine.

Nota: questo perché abbiamo bisogno di trasferire l'intero elenco classificato uno per uno in ogni iterazione, che è O (n). Per ogni componente di ogni tabella, dobbiamo farlo, il che implica che è O (n 2) limitato.

2. Ordinamento bolle

Se la bolla non è nell'ordine richiesto, funziona sostituendo i componenti vicini. Questo viene ripetuto fino a quando tutti i componenti non sono in ordine dall'inizio dell'array. Sappiamo che se riusciamo a eseguire l'intera iterazione senza swap, tutti gli elementi rispetto ai loro elementi adiacenti erano nell'ordine desiderabile e, per estensione, l'intero array. Il motivo dell'algoritmo Bubble Sort è che i numeri come "bolle" nel "terreno". Se, dopo un determinato importo, si passa nuovamente all'istanza (4 è una buona istanza), si noterà che il numero lentamente si sposta a destra.

I passaggi per l'ordinamento delle bolle sono i seguenti:

1. 4 2 1 5 3: qui, i primi due numeri non sono nell'ordine giusto, quindi dobbiamo ordinare entrambi i numeri.
2. 2 4 1 5 3: Dopodiché, anche la prossima coppia di numeri non è nell'ordine giusto. Quindi l'ordinamento si verifica nuovamente.
3. 2 1 4 5 3: questi due sono nell'ordine giusto, 4 <5, quindi non è necessario scambiarli.
4. 2 1 4 5 3 : Ancora una volta dobbiamo scambiare l'ordine corretto.
5. 2 1 4 3 5: ecco l'array risultante dopo una iterazione.
6. Dobbiamo ripetere nuovamente questo processo fino a quando i numeri non sono nell'ordine corretto.

Codice:

public class BubbleSortExample (
public static void bubbleSort(int() arr) (
int n = arr.length;
int tmp = 0;
for(int x=0; x < n; x++)(
for(int y=1; y < (nx); y++)(
if(arr(y-1) > arr(y))(
//swap elements
tmp = arr(y-1);
arr(y-1) = arr(y);
arr(y) = tmp;
)
)
)
)
public static void main(String() args) (
int arr() =(4, 2, 1, 5, 3);
System.out.println("Array Before Bubble Sort");
for(int x=0; x < arr.length; x++)(
System.out.print(arr(x) + " ");
)
System.out.println();
bubbleSort(arr);
System.out.println("Array After Bubble Sort");
for(int x=0; x < arr.length; x++)(
System.out.print(arr(x) + " ");
)
)
)

Produzione:

Nota: potrebbe essere finito in un ciclo infinito se avessi usato a (i)> = a (i + 1), perché quella connessione sarebbe stata ancora valida con componenti equivalenti e quindi li avrei sempre scambiati da un elemento all'altro.

3. Selezione ordinamento

Selezione ordinamento suddivide la matrice in una matrice di classificazioni che non sono ordinate. Questa volta, tuttavia, il subarray di ordinamento viene formato inserendo alla fine dell'array ordinato l'elemento minimo del subarray non ordinato, scambiando:

1. 3 5 1 2 4
2. 1 5 3 2 4
3. 1 2 3 5 4
4. 1 2 3 5 4
5. 1 2 3 4 5
6. 1 2 3 4 5

Codice:

public class SelectionSortEx (
public static void selectionSort(int() arr)(
for (int x = 0; x < arr.length - 1; x++)
(
int indx = x;
for (int y = x + 1; y < arr.length; y++)(
if (arr(y) < arr(indx))(
indx = y;
)
)
int smallNumber = arr(indx);
arr(indx) = arr(x);
arr(x) = smallNumber;
)
)
public static void main(String a())(
int() arr1 = (3, 5, 1, 2, 4);
System.out.println("Before Sorting");
for(int x:arr1)(
System.out.print(x+" ");
)
System.out.println();
selectionSort(arr1);
System.out.println("After Selection Sorting");
for(int x:arr1)(
System.out.print(x+" ");
)
)
)

Produzione:

Nota: il minimo è O (n) per la dimensione dell'array poiché è necessario verificare tutti i componenti. Per ogni elemento dell'array, dobbiamo trovare il minimo e limitare l'intero processo O (n 2).

4. Unisci ordinamento

Unisci ordinamento utilizza la ricorsione per risolvere il problema del metodo di divisione e conquista in modo più efficace rispetto agli algoritmi precedentemente descritti.

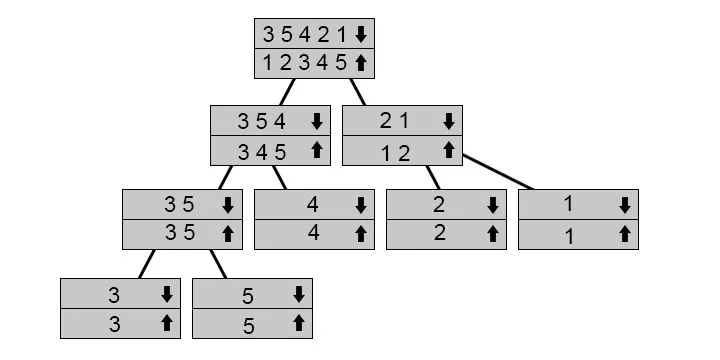
Questo albero mostra come funzionano le chiamate ricorsive. Le matrici contrassegnate con la freccia verso il basso sono le matrici per le quali chiamiamo funzione mentre fondiamo le matrici con le frecce. Quindi segui la freccia sul bordo dell'albero e poi ritorna e unisci. Abbiamo un intervallo di 3 5 3 1, quindi lo dividiamo in 3 5 4 e 2 1. Li dividiamo nelle loro parti per ordinarli. Iniziamo a fonderli e selezionarli mentre procediamo verso il fondo.

Codice:

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
public class MergeSort (
static void merge(int() array, int lowval, int midval, int highval)(
int x, y, k;
int() c= new int(highval-lowval+1);
k = 0;
x=lowval;
y=midval+1;
while(x<=midval && y<=highval)(
if(array(x)<=array(y))(
c(k++) = array(x++);
)
else(
c(k++) = array(y++);
)
)
while(x<=midval)(
c(k++) = array(x++);
)
while(y<=highval)(
c(k++) = array(y++);
)
k=0;
for(x = lowval; x<=highval; x++)(
array(x) = c(k++);
)
)
static void mergeSort(int() array, int lowval, int highval)(
if(highval-lowval+1>1)(
int midval = (lowval+highval)/2;
mergeSort(array, lowval, midval);
mergeSort(array, midval+1, highval);
merge(array, lowval, midval, highval);
)
)
public static void main(String() args) (
BufferedReader r = new BufferedReader(new InputStreamReader(System.in));
int size;
System.out.println("Enter the array");
try (
size = Integer.parseInt(r.readLine());
) catch (Exception e) (
System.out.println("Please Enter valid Input");
return;
)
int() array = new int(size);
System.out.println("Enter array elements");
int x;
for (x = 0; x < array.length; x++) (
try (
array(x) = Integer.parseInt(r.readLine());
) catch (Exception e) (
System.out.println("An error Occurred");
)
)
System.out.println("After Sorting");
System.out.println(Arrays.toString(array));
mergeSort(array, 0, array.length-1);
System.out.println("Before Merge Sorting");
System.out.println(Arrays.toString(array));
)
)

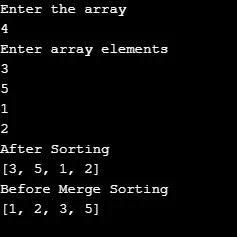
In questo programma, abbiamo chiesto all'utente di inserire l'input. L'output sarà in ordine ordinato in base all'input dell'utente.

Produzione:

5. Ordinamento dell'heap

Devi prima conoscere il framework su cui opera Heapsort, l'heap, per capire perché funziona. Parleremo in particolare di un heap binario, ma puoi anche generalizzare questo ad altre costruzioni di heap. Un heap è un albero che soddisfa le proprietà dell'heap, vale a dire che tutti i suoi figli hanno relazioni con ciascun nodo. Anche un mucchio deve essere quasi finito. Un binario d-depth quasi completo ha una sottostruttura d-1, con la stessa radice, e ogni nodo ha una sottostruttura piena, sinistra, con una sinistra discendente.

In altre parole, si ottiene un numero sempre più basso (min-heap) o più grande e più grande (max-heap) quando ci si sposta giù dall'albero. Ecco un'istanza max-heap:

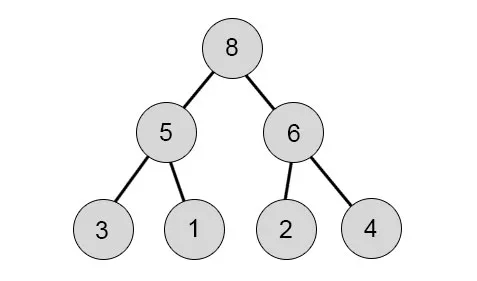
1. 6 1 8 3 5 2 4 : Qui, entrambi i numeri dei bambini sono più piccoli del genitore, quindi non dobbiamo cambiare nulla.
2. 6 1 8 3 5 2 4: Qui, 5> 1, dobbiamo scambiarli. Dobbiamo ammassarci per 5.
3. 6 5 8 3 1 2 4: entrambi i numeri dei bambini sono più piccoli, tutto rimane uguale.
4. 6 5 8 3 1 2 4: qui, 8> 6, quindi dovremmo scambiarli.
5. 8 5 6 3 1 2 4: Dopo questa iterazione, otterremo questo risultato.

Dopo aver ripetuto questo processo, avremo i seguenti risultati:

• 8 5 6 3 1 2 4

1. 4 5 6 3 1 2 8 : Scambio
2. 6 5 4 3 1 2 8 : Heapify
3. 2 5 4 3 1 6 8 : Scambio
4. 5 2 4 2 1 6 8 : Heapify
5. 1 2 4 2 5 6 8 : scambio

Codice:

public class HeapSort
(
public void sort(int arr())
(
int n = arr.length;
for (int x = n / 2 - 1; x >= 0; x--)
heapify(arr, n, x);
for (int x=n-1; x>=0; x--)
int tmp = arr(0);
arr(0) = arr(x);
arr(x) = tmp;
heapify(arr, x, 0);
)
)
void heapify(int arr(), int n, int x)
(
int largest = x;
int L = 2*x + 1;
int r = 2*x + 2;
if (L arr(largest))
largest = L;
if (r arr(largest))
largest = r;
if (largest != x)
(
int swap = arr(x);
arr(x) = arr(largest);
arr(largest) = swap;
heapify(arr, n, largest);
)
)
static void printArray(int arr())
(
int n = arr.length;
for (int x=0; x System.out.print(arr(x)+" ");
System.out.println();
)
public static void main(String args())
(
int arr() = (6, 1, 8, 3, 5, 2, 4);
int n = arr.length;
System.out.println("Before Sorting:");
printArray(arr);
HeapSort ob = new HeapSort();
ob.sort(arr);
System.out.println("After Heap Sorting:");
printArray(arr);
)
) public class HeapSort
(
public void sort(int arr())
(
int n = arr.length;
for (int x = n / 2 - 1; x >= 0; x--)
heapify(arr, n, x);
for (int x=n-1; x>=0; x--)
int tmp = arr(0);
arr(0) = arr(x);
arr(x) = tmp;
heapify(arr, x, 0);
)
)
void heapify(int arr(), int n, int x)
(
int largest = x;
int L = 2*x + 1;
int r = 2*x + 2;
if (L arr(largest))
largest = L;
if (r arr(largest))
largest = r;
if (largest != x)
(
int swap = arr(x);
arr(x) = arr(largest);
arr(largest) = swap;
heapify(arr, n, largest);
)
)
static void printArray(int arr())
(
int n = arr.length;
for (int x=0; x System.out.print(arr(x)+" ");
System.out.println();
)
public static void main(String args())
(
int arr() = (6, 1, 8, 3, 5, 2, 4);
int n = arr.length;
System.out.println("Before Sorting:");
printArray(arr);
HeapSort ob = new HeapSort();
ob.sort(arr);
System.out.println("After Heap Sorting:");
printArray(arr);
)
)

Produzione:

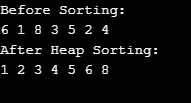
Puoi vederlo da un punto all'altro del grafico, da sinistra a destra. Ciò che abbiamo ottenuto qui è che quando abbiamo il componente kth nell'array, la posizione dei suoi figli è 2 \ * k + 1 e 2 \ * k + 2 (supponendo che l'indicizzazione inizi da 0). Questo può essere monitorato da te. La posizione del genitore è sempre (k-1) / 2 per il componente kth. Puoi prontamente "ammassare al massimo" qualsiasi intervallo, perché lo sai. Controlla se uno dei suoi figli è inferiore a quello di ciascun componente. In tal caso, associare un genitore e ripetere questo passaggio in modo ricorsivo con il genitore.

Nota: poiché iterando i cicli for nell'intero array rende heapSort) (ovviamente O (N), creerebbe la complessità complessiva di Heapsort O (nlog n). Heapsort ha un tipo sul posto, il che significa che richiede O ( 1) più spazio di Merge Sort, ma presenta alcuni svantaggi, come i parallelismi che sono difficili.

Conclusione - Ordinamento degli algoritmi in Java

L'ordinamento è una procedura molto diffusa con set di dati, sia per ulteriori analisi, che accelera la ricerca con algoritmi più efficaci basandosi su informazioni ordinate, filtrando informazioni, ecc. L'ordinamento è approvato da diverse lingue e spesso le interfacce oscurano ciò che fa il programmatore.

Articoli consigliati

Questa è una guida per ordinare gli algoritmi in Java. Qui discutiamo diversi tipi di ordinamento in Java insieme ai loro algoritmi. Puoi anche consultare i nostri altri articoli suggeriti:

1. Unisci gli algoritmi di ordinamento in Java
2. JComboBox in Java
3. StringBuffer in Java
4. JTextField in Java
5. Ordinamento dell'heap in Python
6. Algoritmi di ordinamento rapido in Java
7. Guida completa all'ordinamento in C # con esempi
8. Ordinamento degli algoritmi in JavaScript
9. Guida agli esempi di algoritmo C ++
10. Guida completa all'ordinamento degli algoritmi in Python