Introduzione a Heap Sort in C
L'ordinamento è una tecnica che riguarda tutto l'ordinamento di elementi in base a proprietà diverse. (Proprietà come la disposizione dei dati in ordine crescente, decrescente o alfabetico). Un esempio importante di ordinamento che possiamo pensare qui è l'ordinamento di articoli durante lo shopping online. Possiamo fare riferimento a prezzi, popolarità, ultime e così via. Quindi ci sono molte tecniche per questo posizionamento degli elementi attraverso l'ordinamento. In questo argomento, impareremo l'ordinamento degli heap in C.
Qui impareremo una delle tecniche di ordinamento più comuni, Heap Sort, attraverso il linguaggio di programmazione C.
La logica per l'heap sort
Come possiamo effettivamente eseguire l'heap sort? Diamo un'occhiata qui sotto.
Innanzitutto, l'heap è una struttura di dati basata su alberi. L'albero coinvolto qui è sempre un albero binario completo. E ci sono due tipi di heap
- Min - Heap: generalmente disposti in ordine crescente, cioè se l'elemento del nodo padre ha un valore inferiore a quello degli elementi del nodo figlio.
- Max - Heap: generalmente disposti in ordine decrescente, ovvero se l'elemento del nodo padre ha un valore superiore a quello degli elementi del nodo figlio.
Passaggi per l'ordinamento dell'heap
- Una volta ottenuti i dati di un elenco non ordinato, gli elementi vengono organizzati nella struttura dei dati dell'heap in base alla creazione di un min-heap o di un max-heap.
- Il primo elemento dell'elenco precedente viene aggiunto al nostro array
- Anche in questo caso la tecnica della struttura dei dati di testa è la stessa del primo passo e di nuovo l'elemento più alto o il minimo viene raccolto e aggiunto nel nostro array.
- I passaggi ripetuti ci aiutano a ottenere l'array con l'elenco ordinato.
Programma per Heap Sort in C
#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)
Innanzitutto, chiediamo all'utente di inserire il numero di elementi presi per l'ordinamento e quindi all'utente è consentito inserire diversi elementi che devono essere ordinati.
Passaggi Seguiti
- Il prossimo su cui ci stiamo concentrando è la creazione di un array heap, in questo caso, l'array max-heap.
- La condizione principale per ottenere un array max - heap è verificare che nessun valore del nodo padre sia inferiore al suo valore del nodo figlio. Sostituiremo fino a quando non raggiungeremo tale condizione.
- Il vantaggio principale in questo albero binario completo è che è possibile accedere ai nodi figlio sinistro e destro di un nodo padre con i valori 2 (i) + 1 e 2 * (i) + 2 rispettivamente. Dove sono il nodo principale.
- Quindi, in questo modo, stiamo posizionando il nostro nodo radice che contiene il valore massimo nella posizione del nodo foglia più a destra. E poi di nuovo seguendo la stessa procedura in modo che il prossimo numero massimo diventi ora il nodo principale.
- Seguiremo la stessa procedura fino a quando nell'array di heap rimane solo un nodo.
- E poi, stiamo organizzando il nostro array di heap per formare un array ordinato perfetto in ordine crescente.
- Infine, stiamo stampando l'array ordinato nell'output.
Produzione:
L'output è allegato di seguito.
Lascia che ti mostri la rappresentazione pittorica degli avvenimenti:
- I dati immessi vengono prima rappresentati sotto forma di un array monodimensionale come segue.

- La rappresentazione pittorica dell'albero binario formato è la seguente:
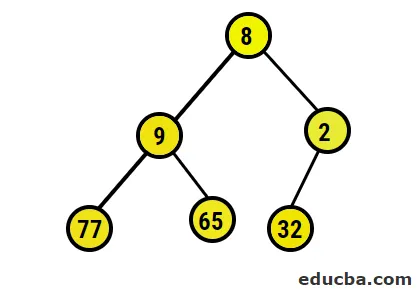
- Ora eseguiremo la conversione nell'heap massimo assicurandoci che tutti i nodi padre siano sempre maggiori dei nodi figlio. Come menzionato nell'output nell'array ordinato heap, la rappresentazione pittorica sarebbe:
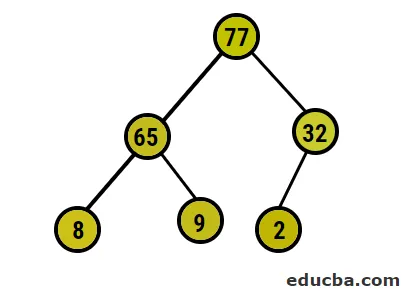
- Successivamente, sostituiremo il nodo radice con il nodo foglia estremo e lo elimineremo dall'albero. Il nodo foglia sarebbe la radice di tanto in tanto lo stesso processo seguito per ottenere di nuovo l'elemento più alto nella radice
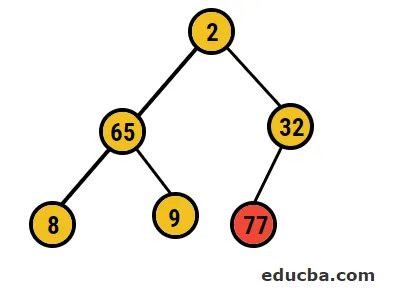
- Quindi, in questo caso, 77 cifre vengono eliminate da questo albero e inserite nel nostro array ordinato e il processo viene ripetuto.
Quanto sopra l'abbiamo visto per formare l'array heap max. Lo stesso processo si occupa anche della formazione dell'array min-heap. Come discusso in precedenza, l'unica differenza è con la relazione tra elementi del nodo padre e figlio.
Come esercizio, puoi provare a formare l'heap in ordine decrescente?
Conclusione
Sebbene esistano molte tecniche di ordinamento, l'heap ordinamento è considerato una delle migliori tecniche di ordinamento grazie alla sua complessità temporale e spaziale. La complessità temporale per tutti i casi migliori, medi e peggiori è O (nlogn), dove la complessità peggiore è migliore della complessità peggiore di Quicksort e la complessità spaziale è O (1).
Articoli consigliati
Questa è una guida per l'ordinamento dell'heap in C. Qui discutiamo la logica e i passaggi per l'ordinamento dell'heap con il codice di esempio e l'output insieme a rappresentazioni pittoriche. Puoi anche dare un'occhiata ai seguenti articoli per saperne di più -
- Ordinamento dell'heap in Java
- Selezione ordinamento in Java
- Programma Palindrome in C.
- Pattern nella programmazione C.
- Ordinamento dell'heap in C ++ (algoritmo)
- Ordinamento dell'heap in Python
- C Moltiplicazione della matrice di programmazione