
Formula di deviazione standard di esempio (sommario)
- Formula
- Esempi
Formula di deviazione standard del campione
In statistica, la deviazione standard è sostanzialmente una misura per trovare la dispersione dei valori del set di dati dal valore medio del set di dati. Misura la distanza di quel punto dati e la media. Quindi più alta è la deviazione standard, maggiore sarà la dispersione e i punti dati tenderanno ad allontanarsi dalla media. Allo stesso modo, una deviazione standard più bassa significa che i punti dati saranno più vicini alla media. È molto utile nel confronto di set di dati che possono avere lo stesso valore medio ma un intervallo diverso.
Di solito, calcolare la deviazione standard dei dati sulla popolazione, ma a volte i dati sulla popolazione sono così enormi che non è possibile trovare la deviazione standard per quello. In tal caso, viene calcolata la deviazione standard del campione che diventerà il rappresentante della deviazione standard della popolazione. Quindi supponiamo che il campione sia la rappresentazione corretta della popolazione e ci concentreremo sulla deviazione standard del campione in questo articolo.
Supponiamo di avere un set di dati X con punti dati (X1, X2 …… ..Xn).
La formula per la deviazione standard della popolazione è data da:
Population Standard Deviation = √ (Σ (X i – X m ) 2 / n )
Nel caso in cui non ti venga data l'intera popolazione e hai solo un campione (supponiamo che X sia il set di dati campione della popolazione), la formula per la deviazione standard del campione è data da:
Sample Standard Deviation = √ (Σ (X i – X m ) 2 / (n – 1))
Dove:
- X i - i valore del set di dati
- X m - Valore medio del set di dati
- n - Numero totale di punti dati
La formula può sembrare inizialmente confusa, ma è davvero su cui lavorare. Di seguito sono riportati i passaggi che è possibile seguire per calcolare la deviazione standard del campione:
- Trova il numero di punti nel set di dati, ad es. N
- Quindi il passo successivo è trovare il valore medio del campione. È fondamentalmente la media di tutti i valori.
- Dopodiché, per ogni punto dati, trova la differenza rispetto alla media e quindi quadrala.
- Prendi la somma di tutti i valori nel passaggio precedente e dividi quello per n-1.
- L'ultimo passo è prendere la radice quadrata del numero calcolato sopra.
Esiste un altro modo per calcolare la deviazione standard e della popolazione semplicemente usando la funzione STDEV.P () per la deviazione standard della popolazione e la funzione STDEV.S () per la deviazione standard del campione in Excel.
Esempi di formula di deviazione standard di esempio (con modello Excel)
Facciamo un esempio per comprendere meglio il calcolo della deviazione standard del campione.
Puoi scaricare questo modello Excel di esempio di formula di deviazione standard qui - Modello Excel di esempio di formula di deviazione standardFormula di deviazione standard del campione - Esempio n. 1
Diciamo che abbiamo due set di dati di esempio A e B e ognuno contiene 20 punti di dati casuali e ha la stessa media. Calcola la deviazione standard del campione per il set di dati A e B.
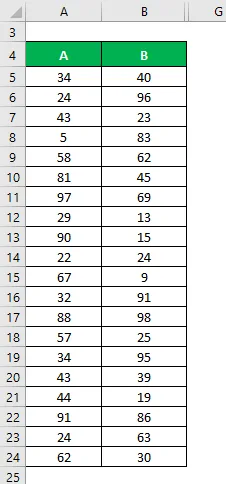
Soluzione:
La media è calcolata come:
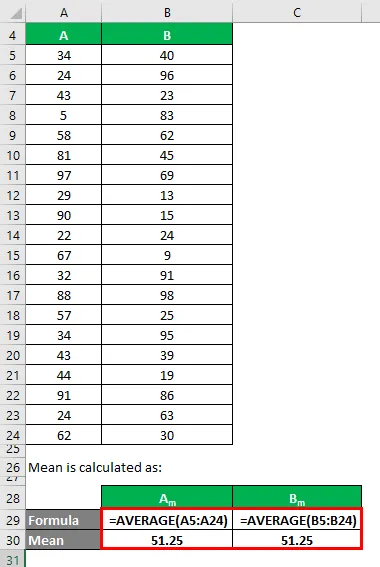
- Media del set di dati A = 51, 25
- Media del set di dati B = 51, 25
Ora, dobbiamo calcolare la differenza tra i punti dati e il valore medio.
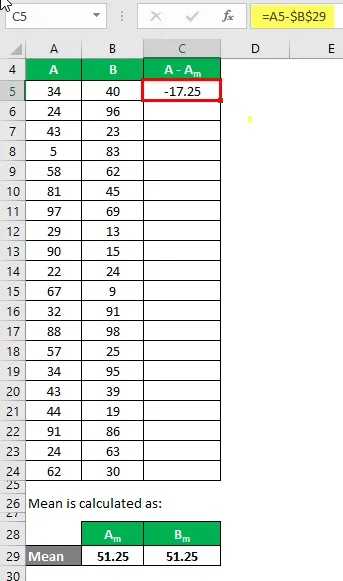
Allo stesso modo, calcolare per tutti i set di dati di A.
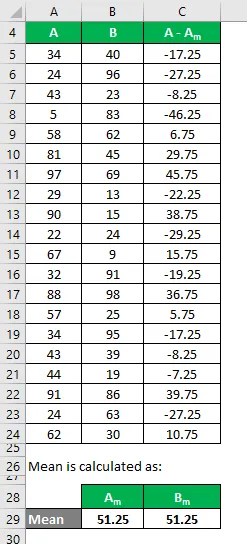
Allo stesso modo, calcolarlo anche per il set di dati B.
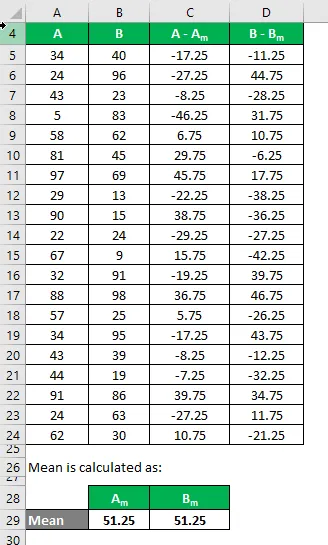
Calcola il quadrato della differenza per entrambi i set di dati A e B.
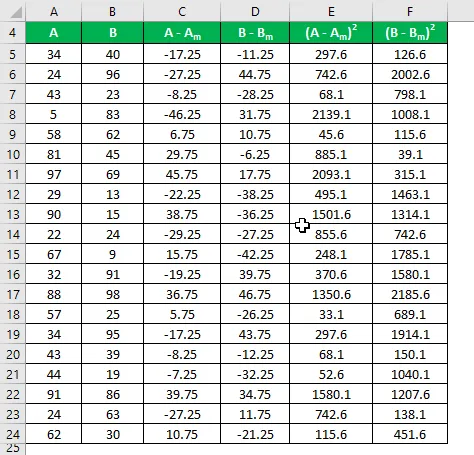
La deviazione standard del campione viene calcolata utilizzando la formula indicata di seguito
Deviazione standard del campione = √ (Σ (X i - X m ) 2 / (n - 1))
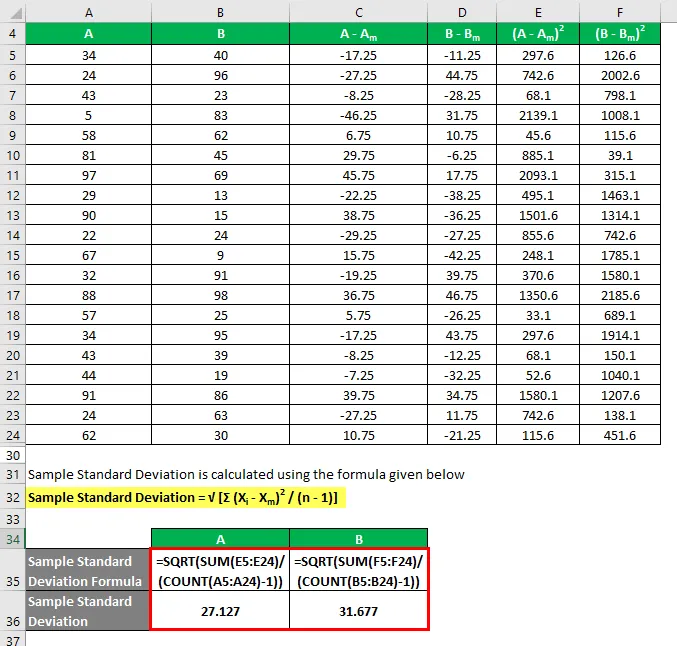
Quindi, se vedi qui, sebbene entrambi i set di dati abbiano lo stesso valore medio, B ha una deviazione più standard di A, il che significa che i punti di dati di B sono più dispersi di A.
Formula di deviazione standard del campione - Esempio n. 2
Diciamo che sei un investitore molto avverso al rischio e stai cercando di investire denaro nel mercato azionario. Poiché la tua propensione al rischio è bassa, vuoi investire in titoli sicuri che hanno una deviazione standard inferiore. Il tuo consulente finanziario ti ha suggerito 4 titoli tra cui puoi scegliere. Volete selezionare 2 titoli tra quelli 4 e lo deciderete sulla base di una deviazione standard inferiore.
Hai informazioni sui loro rendimenti storici negli ultimi 15 anni.
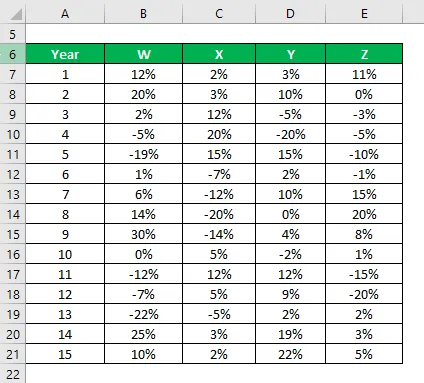
Soluzione:
La deviazione standard del campione viene calcolata utilizzando la formula di Excel
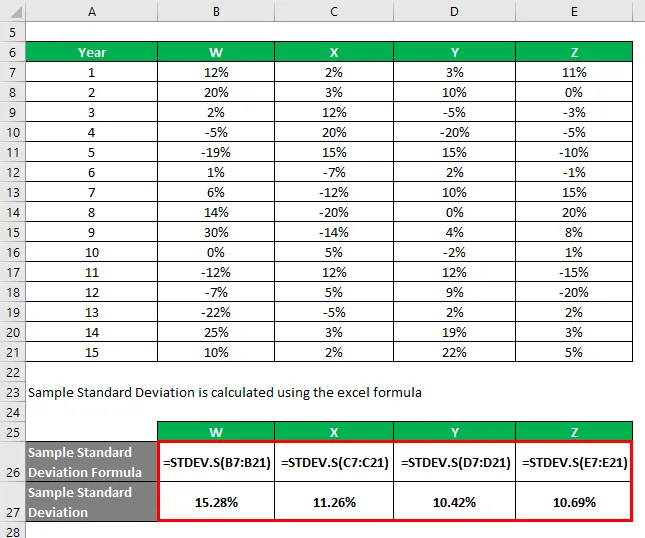
In base alle informazioni e alla deviazione standard del campione, sceglierai le azioni Y e Z da investire poiché presentano la deviazione standard più bassa.
Spiegazione
Discutiamo il significato della deviazione standard da un punto di vista statistico, ma svolge anche un ruolo vitale se parliamo di un punto di vista finanziario. Nel settore finanziario, è fondamentalmente la misura del rischio che comporta un investimento e quanto sia rischioso tale investimento. Sulla base del rischio di un investimento, gli investitori possono quindi calcolare il rendimento minimo necessario per compensare tale rischio. Come nell'esempio sopra, poiché Y e Z hanno una deviazione standard minore, significa che c'è una minore variabilità nel rendimento di questi titoli, quindi sono meno rischiosi. Un punto durante l'utilizzo dello strumento di deviazione standard è necessario tenere presente che è fortemente influenzato da valori estremi o valori anomali. Questi valori anomali possono distorcere il valore di deviazione standard.
Rilevanza e usi della formula di deviazione standard del campione
La deviazione standard aiuta gli investitori e l'analista a trovare il rapporto rischio / rendimento o il rapporto Sharpe per un investimento. Fondamentalmente, chiunque può guadagnare un tasso di rendimento privo di rischio investendo in titoli del Tesoro e privi di rischio. Ma il rendimento oltre a questo è l'eccesso di rendimento e per raggiungere ciò, qual è il livello di rischio che uno deve prendere è una misura del rapporto di Sharpe:
Sharpe Ratio = (Return on Investment - Risk Free Rate) / Deviazione standard
Per aumentare il rapporto di Sharpe, migliore è l'investimento.
Come abbiamo detto, la deviazione standard è una misura del rischio, ma non è sempre preferibile un valore di deviazione standard inferiore. Se un investitore ha una maggiore propensione al rischio e desidera investire in modo più aggressivo, sarà disposto a correre più rischi e preferirà una deviazione standard relativamente più elevata rispetto a un investitore avverso al rischio. Quindi tutto dipende dal livello di rischio che un investitore è disposto a correre.
Articoli consigliati
Questa è stata una guida alla Formula di deviazione standard del campione. Qui discutiamo come calcolare la deviazione standard del campione insieme ad esempi pratici e template Excel scaricabili. Puoi anche consultare i seguenti articoli per saperne di più -
- Esempi di formula di varianza della popolazione
- Calcolatrice per deviazione standard relativa
- Come calcolare la distribuzione normale standard?
- Calcolo della distribuzione binomiale